Writing an optimizing tensor compiler from scratch





|
|---|
In this blog post I want to talk about the research and development results for a library that I started working on more than a year ago - TensorFrost. Under the hood it’s a static optimizing tensor compiler with a focus on being able to do more “shader-like” things while still keeping the ability to do high level linear algebra for ML in Numpy-like syntax with automatic differentiation support. (Click on the example GIF’s for more details!)
For documentation on basic functionality, read the README file in the repo.
- So why make a new library?
- Architecture
- Python frontend
- Backends
- Examples using TensorFrost
- What’s the current performance compared to other tensor libraries?
- What is left to do
- Conclusion
I started working on this library around 14 months ago, initially I didn’t really plan to do much more than a few matrix operations for an optimization algorithm I wanted to implement in Unity, but there were quite a few things that I wanted to have on top of all of this and it sidetracked me into a writing an entire compiler (hello scope creep 👋).
The thing is, it’s not the first time I tried to make a tensor library, the first time was a whole 5 years ago and used OpenCL, as I didn’t have an Nvidia GPU at the time. To be honest I’ve been completely unprepared to the magnitude of what it required, and while I did get it to a “somewhat” working state like having basic kernels and somewhat working autodiff using a tape, the lack of good debug tools and actual problems that I wanted to solve pretty much killed it. And for the things that I did want to work on, it was completely unsuited for, as I usually write simulations or graphics, and the overhead of doing a kernel per operation (especially unoptimized kernels) is just too bad to be useful.
Since that time I’ve had a lot of ideas of what I would like a library like that to even look like, and wanted to try working on it again. However I did know, that for this project to survive I would need to make it suitable for projects I usually do, like the ones I usually do on Shadertoy. It might seem weird to you as to why I would make a specifically “tensor” library for something that is basically equivalent to writing shaders. But to be honest, shaders are not actually a perfect place for what I do, and a lot of simulation/rendering algorithms can map quite well to high level “tensor-like” operations. While the limitations might force you to come up with creative solutions, for really large or complicated projects it just becomes more of a problem, as it’s very hard to iterate on quickly. This was also one of the main reasons I didn’t really touch ML too much for most of my pet projects (except stuff like Neural Implicit Representations), ML algorithms are usually quite orthogonal to the way you write shaders, usually being split into hundreds of kernel dispatches, while those shader algorithms are effectively just one megakernel most of the time. The only reasonable way to integrate neural networks into those is unrolling the network into a single scalar function, which can be quite unoptimal and limits their size. Not even talking about the fact that training them is completely out of the question. This brings up another problem, shaders don’t have automatic differentiation, which is surprisingly much more useful here than you might think. While its usually used for optimization algorithms like SGD, having the analytic gradient can also be useful for computing normals/curvature of analytic shapes, or forces from potentials in simulations.
So in this library, I hoped to somehow extend the applicability range of a Tensor library to more “shader-like” use cases like rendering and simulations.
And right now I can actually say that at least to some partial degree it did work out. Currently the library is something of a mix of slightly more low-level Numpy-like operations with shader-like control-flow and operations (most of the built-in scalar shader functions are passed through to Python). In terms of where it stands right now, its more low-level than something like JAX or PyTorch, but still not as low-level as Taichi as you still technically operate on something similar to tensors.

So why make a new library?

It will indeed take a inordinate amount of work to make a library from scratch and get it to a useful state, as I’ve already experienced. Why would I not just use an existing library, as there are seemingly thousands of them? There are a few reasons mostly applicable to my use cases which make both using pure ML libraries or pure shaders annoying.
1. Performance scales poorly for non-ML specific operations
Of course, nothing stops me from using your usual ML libraries like PyTorch or JAX, but as I mentioned before, they weren’t really designed to be applied to problems that I have. These libraries effectively live in their own realm with their own rules and syntax fine tuned for ML, and hide some of the features the GPU has from the user, they pretty much have 0 crossover with how shaders operate. While technically you can write any algorithm you want in plain tensors, including graphics and simulations, depending on the number or complexity of operations - the performance could get terrible.
Most of the Tensor compiler research that I’ve seen focuses on ML bottlenecks, like efficiently utilizing cache, correctly aligning data for maximum performance of matrix multiplications, convolutions etc. Those usually aren’t a bottleneck when dealing with simulations or rendering, the bottleneck becomes the dynamic nature of the code and its complexity.
2. Dynamic control flow is very tedious (if possible) to implement in classic ML libraries
The performance is actually not the only issue when writing simulations or graphics, control flow can be very prevalent, but unfortunately it’s quite inconvenient to express in these libraries, if even possible, as native loops in JAX for example, require doing stuff like:
def factorial(n):
def cond_fun(state):
i, fact = state
return i < n
def body_fun(state):
i, fact = state
return i + 1, fact * (i + 1)
initial_state = (0, 1)
final_state = jax.lax.while_loop(cond_fun, body_fun, initial_state)
return final_state[1]
Which looks completely cursed. Now imagine multiple stacked loops - yikes
Such native loops are required if you want a varying iteration count for some operation, in simulations this could be, for example, summing a force from a varying number of particle neighbors. Even something like Gaussian Splatting requires a variable loop per tile. From a purely classic ML standpoint, this isn’t really a problem, since such cases practically never happen and the computational graph is absolutely static, and whats worse, autodiff gradients of such loops might potentially have atrocious performance (or might just be uncomputable if the loop can be theoretically infinite, as the compiler might not know the specific context where its being used).
You could alternatively write a dynamic mask that will depend on the iteration, and unroll the loop, but this would simply be slower and less readable. Like here, I once tried to make a vectorized Numpy function to computes the mandelbulb SDF:
def mandelbulb_sdf(pos, iter_num=mandelbulb_iter_num, power=mandelbulb_power):
z = pos
dr = 1.0
r = 0.0
for i in range(iter_num):
r = np.linalg.norm(z, axis=-1)
not_mask = ~(r > 1.5)
theta = np.arccos(z[..., 2] / r)
phi = np.arctan2(z[..., 1], z[..., 0])
dr = np.where(not_mask, r**(power - 1.0) * power * dr + 1.0, dr)
zr = r**power
theta *= power
phi *= power
z = np.where(not_mask[:, :, :, np.newaxis], pos + zr[:, :, :, np.newaxis] * np.array([np.sin(theta) * np.cos(phi), np.sin(theta) * np.sin(phi), np.cos(theta)]).transpose(1, 2, 3, 0), z)
return 0.5 * np.log(r) * r / dr
3. Extending ML libraries with custom high-performance kernels requires using external tools/APIs like CUDA or Triton
Usually, when hitting a performance bottleneck, you have to write custom CUDA kernels, which is doable, but quite inconvenient, as it forces you to use separate environments, CUDA and Python.
There are actually domain specific languages (DSLs) that allow you to write kernels in relatively high-level Python, like Taichi or Nvidia’s Warp, they are really nice for simulations or graphics, and Taichi specifically is fine tuned for high performance physics simulations and even has built in automatically optimized sparse grids. And while they are also differentiable, they still are a bit off from what I would consider “perfect”, as you don’t have access to the giant library of ML operations that PyTorch has for example. Of course you can still write ML using them if you really want, there are some Nerf implementations for Taichi, but they require much more code to represent. As a compromise you could also interoperate them with PyTorch for example, but once again, it makes it less convenient to work with. I can also mention Triton here, but it’s usually used more like a backend for other libraries (like PyTorch) rather than a standalone DSL, at least as far as I have seen.
There is also Slang, which is quite different from all these from above, as its an improved shader language with added differentiability. It would be nice if it was widely supported. But its even more low level than something like Taichi.
4. ML libraries don’t have an easy built-in way to make real-time visualizations with optional interactivity
When I want to do some advanced visualizations in Python, the options that are available in ML libraries are often hilariously bad. Usually you just end up making a bunch of matplotlib plots, which are not only slow, if you want to render like hundreds of millions of points or an animation, but also not interactive. (They are fine for papers tho)
In the world of real-time graphics, you can render those points at 60fps, and you could even interact with them in real time. Seeing the things you are working on in real time is in some cases quite useful for quick iteration, and I feel like this is something you miss in your classic ML libs, where the usual interaction you have with your model - is staring at the loss graph for hours.
Though, while I am stating these things, most large ML models are simply not visualizable in real time, and the ones that are, are usually not easy to usefully interpret. Visualizations are usually most applicable to the intersection of ML/Physics/Graphics, like NERFs, diffusion, neural implicit representations, etc. But I still think that even changing hyperparameters in real time and seeing its result on the training loss can also be somewhat interesting, though you do need the model to be rather performant for that.
The lack of a native way to output graphical data from these libraries is even more annoying when you remember that GPU’s are called Graphics Processing Units, not Tensor Processing Units. And they have all the required hardware to work with and output graphics.
PS. Taichi actually does have a way to this! It has integration with GLFW and ImGUI.
5. Writing simulations or graphics in a high-level language is could be much easier to iterate on rather than in pure shaders
On the other side, in the world of real-time simulations and graphics, I’ve written custom kernels for every specific algorithm something needed: radix sorts, linear solvers, numerical integrators, etc. So when I’m prototyping or having a new idea how to optimize the algorithm globally, it can get annoying to make global changes in the code structure, since they usually require a partial rewrite, creating new kernels and so on, and I don’t really see why this couldn’t be automated from higher-level operations.
In the end I was wondering: can I somehow combine the best of both worlds? Being able to do both Numpy-like operations while also doing more shader-like things in one place sounds somewhat impossible on paper, but I thought that maybe if you tuned the kernel generation algorithm to specifically be optimal for shader-like operation it might at least work for my use cases? Afterwards I could still support ML use cases well enough even if I just shoehorned the matmul/reduction/convolution kernels separately.
And even if it is impossible, combining everything into a single language would be nice, because the GPU development infrastructure is scattered all over the place, some features are available only in some places, while others are not, they can sometimes not even be interoperable. The development environments are completely separate, there are ML-specific debug tools on Linux, and graphics API specific debug tools on Windows only - and all of these things are using the same hardware - the GPU!
Architecture
Kernel fusion
When thinking about the architecture of what a library like this could be, I’ve first thought from the point of view of simple per-element operations and indexing. Nothing really stops you from writing Numpy code as if it was a shader, for example. However that would be extremely slow, why? Numpy usually executes a single operation over the entire tensor at a time, i.e. loads the data, does the single operation, then puts it back into memory. For a modern computer this is extremely inefficient, since the bandwidth and latency of system memory are nowhere near sufficient to keep up with the computational power of the processor. If you want to utilize all available resources - you need to utilize the cache hierarchy to its full extent. If you could cache intermediate results close to the ALU’s of the processor and keep the intermediate results as long as possible there, you could get a massive speedup by reducing latencies by orders of magnitude. This is why modern processors have multiple levels of cache - they try to solve the issue of memory improvements not keeping up with increasing performance. As a matter of fact since 2017 top tier consumer GPU memory bandwidth has only increased from 500Gb/s to 1Tb/s, while performance has spiked from 10 TFlops to 80 TFlops.
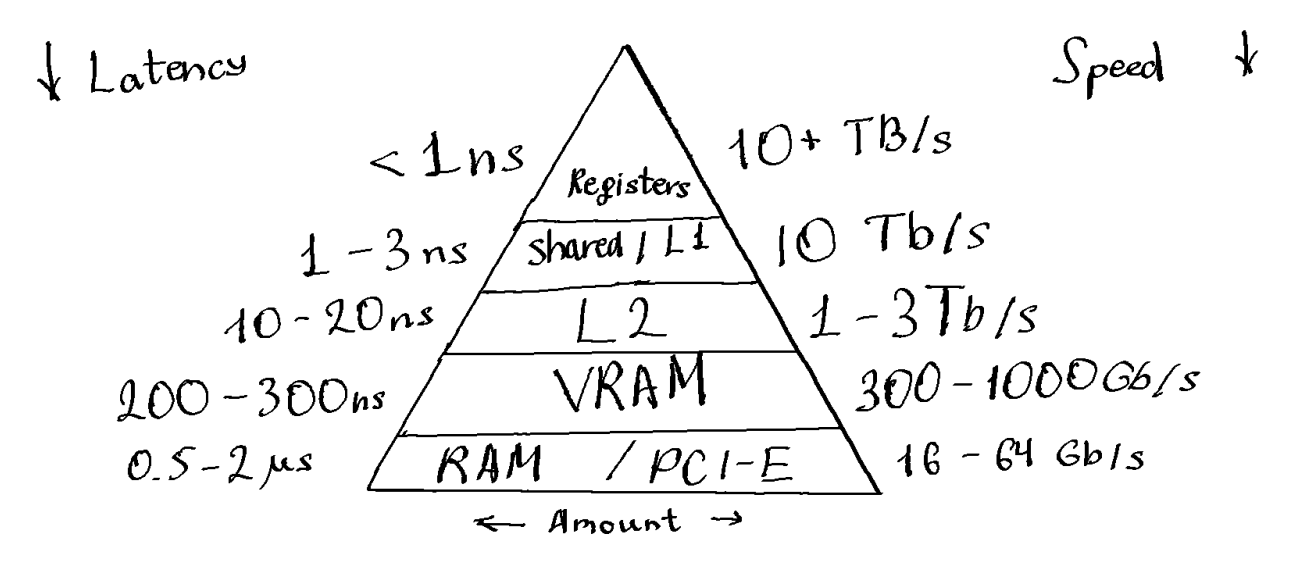 |
|---|
| Tiers of memory of a typical GPU |
But optimizing this specific aspect when dealing with tensors is actually nothing new, the so called kernel fusion has been around for a while, and is used in tensor compilers like XLA or PyTorch’s TorchInductor. And the degree to which they can do it is perfectly fine for most ML applications. However, to my knowledge, they do not fuse operations with already existing optimized kernels, even though in some cases this might be beneficial (Well, in TorchInductor there are only 2 operations that don’t - conv and matmul).
If you tried to write algorithms, like the ones I write in Shadertoy, you will eventually start to hit the limits these compilers have. The number of operation nodes you could fuse now rises to the order of thousands, not even mentioning the complex control flow, and ideally they should fit into a single kernel, but its highly likely you will end up with a lot of smaller kernels if you apply fusion naively.
First prototype
When I initally started prototyping the operation graph compiler in C# in Unity (not exactly your typical place for a compiler prototype, I know), I kept the graph just as a simple Directed Acyclic Graph (DAG), where each node was a single operation with some tensor shape. When I began testing the kernel clustering even on simple physics or rendering, the clustering algorithm quickly started to get out of hand.
Here is an example of a compiled graph with the kernels clusterized.
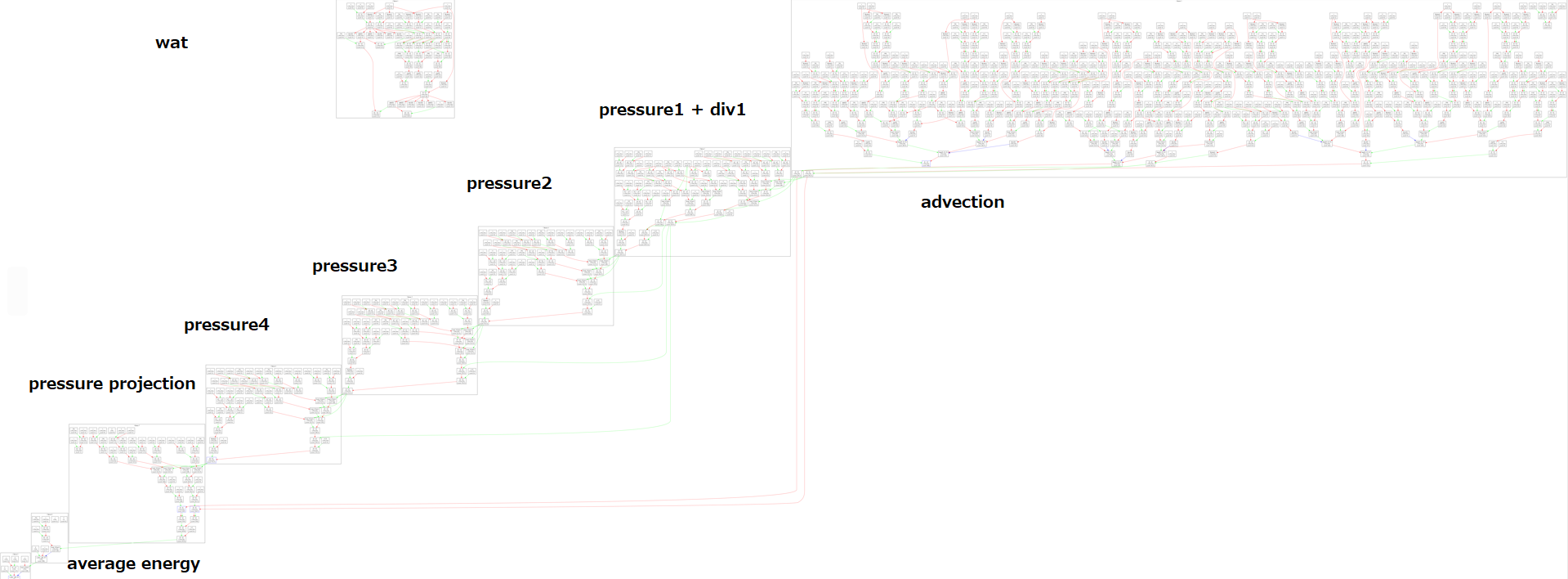
This was the operation/kernel cluster graph for this fluid simulation:
It did work, unfortunately there was no good way to procedurally generate shader code in Unity, so I did something rather stupid and implemented a Virtual Machine right in the shader, which made it particularly slow. However, of the good things, there was practically 0 compile time, but unforuntately that was not the goal I had in mind. The way I did reductions to get the average energy here was also rather questionable - I did it purely with atomics. For some cases they are good, but reduction is not one of them. Especially given that there are no natively supported float atomics in HLSL, so you need to emulate them through InterlockedExchangeCompare, which makes it even slower for this particular use case. One time it even crashed my computer when trying to add a few million floats in parallel to a single element.
The VM basically only knows of 1 dimensional loads and stores, so I also needed to add a compilation stage that converts multidimensional indices into operations that compute the “flattened” index.
At this point the graph had only a few operation types, and I implemented backward-mode autodiff here, which was surprisingly easy. The only not super obvious thing initially was load/store gradients. But those are effectively just atomic_add/load respectively. So in theory, you could implement any ML algorithm even here, but that would be comically slow. Matrix multiplication gradient would be 2 atomic adds per thread in a 3D kernel.
Another thing that turned out to be a huge problem was that the operation graph did not have a “stable” order, it was only topologically sorted (I actually resorted it every time I did something with the graph!), which is good for normal operations, but for inplace operations like stores and atomics this leads to randomly varying results, which is a no-go.
Adding the problem of exponentially growing number of possible kernel fusions and the graphs quicky became an undebuggable node soup, which made this approach not very appealing:
I also wanted to have at least some sort of control flow, which wasn’t obvious how to add into this specific graph for me, at the time.
Second prototype
Any sufficiently complicated C or Fortran program contains an ad hoc, informally-specified, bug-ridden, slow implementation of half of Common Lisp.
This time I wrote it in C++ and decided to instead enforce the order of operations to make in-place operations have properly specified order. I constructed the IR like a linked list, order of which is taken from the way the code is parsed. This simplifies the kernel fusion problem to one of finding ranges of fusable operations, and in my case I fuse everything except any node pair that violated rules based on order of memory access, shape of the operations, etc. In some cases this effectively can convert the entire graph into a single kernel, which is exactly what I’m looking for.
Ordering the operations is not the only thing. To implement control flow I needed to have child and parent nodes while still keeping a uniquely specified ordering, I implemented this by using a multi-level linked list. This way operaitons controlled by a conditional statement or by loops become its children. In multi-level linked lists kernel fusion becomes slightly more tricky, but effectively its just a recursive process of finding the ranges of fusable operations starting from the lowest level of the list, and fusing them level by level.
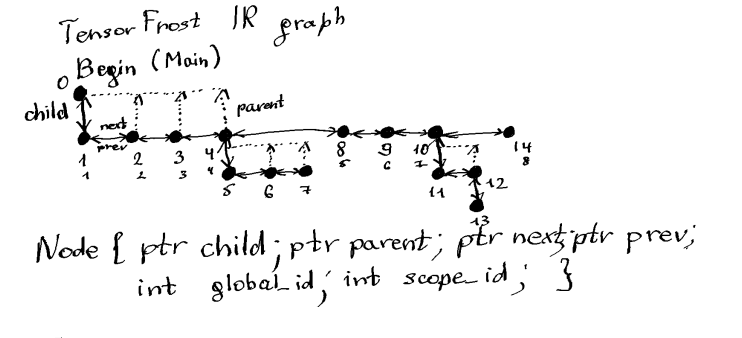
Having children or parents for a tensor is a rather unusual notion, but it is totally fine as long as you make sure that the shape of this node is broadcastable to all of its parents. So you can, for example, have a scalar loop with children of any shape. Or, lets look at a more complex example, a loop of shape [N, 1], with a child loop of shape [] with a child load operation of shape [M]. Totally different shapes, but they are all broadcastable between each other so the shape a generated kernel here will be [N, M] for all these nodes. There are also cases when you have broadcastable shape between parents and children and incompatible shape between neighbors - those are simply incorrect and should lead to a compilation error, as there is no way to generate a kernel here without complex masking, which I don’t plan to support now. Example would be a loop of shape [N] with 2 children of shape [5, N] and [2, N].
The kernels are also represented in the same IR, as children of a “kernel” node. At the code generation stage, everything outside of the kernel nodes is converted into host code (right now C++), and the kernels are converted into device code (OpenMP C++ or GLSL/HLSL). This way the entire program is represented in a single IR, and the compiler can optimize it globally both for CPU and GPU parts.
Since the IR is the same for all compilation stages, you could for example input both high level tensor operations together with explicitly specified kernels, and it can already be done like this:
A = tf.input([-1, -1], tf.float32)
B = tf.input(A.shape, tf.float32)
C = tf.buffer(A.shape, tf.float32)
with tf.kernel(A.shape) as (i, j):
C[i, j] = A[i, j] + B[i, j]
C = (C @ A.T) + tf.unsqueeze(tf.sum(tf.sin(B @ A),axis=-1),axis=-1)
This is already quite nice. (I’ll explain the Python syntax a bit later)
(Note: of course, if you tried to compute the gradient here, the compiler would fail, at least at this point in time, as general gradients over control flow are not trivial)
Another interesting aspect of this representation is that kernels can be created as children of control flow nodes, meaning you can create a loop of kernels for an iterative algorithm, like for example a bitonic sort!
log2N = tf.ceil(tf.log2(tf.float(element_count)))
Nround = tf.int(tf.exp2(log2N))
sort_id = tf.indices([Nround/2])[0]
steps = tf.int(log2N*(log2N + 1.0)/2.0)
with tf.loop(steps) as step:
j = tf.floor(tf.sqrt(tf.float(2*step) + 1.0) - 0.5)
n = tf.round(tf.float(step) - 0.5*j*(j+1.0))
B = tf.int(tf.round(tf.exp2(j-n)))
mask = tf.select(n < 0.5, 2*B - 1, B)
e1 = sort_id%B + 2*B*(sort_id/B)
e2 = e1 ^ mask
with tf.if_cond((e1 < element_count) & (e2 < element_count)):
key1, key2 = keys[e1], keys[e2]
with tf.if_cond(key1 < key2):
val1, val2 = values[e1], values[e2]
keys[e1] = key2
keys[e2] = key1
values[e1] = val2
values[e2] = val1
In this case the compiler can spot that you can’t fuse the insides of the loop since they are reading and writing from the same memory, thus creating a kernel region under the loop.
However, while you can do that, in this particular case, I woudn’t recommend relying on the compiler too much, and would put an explicit kernel under the loop, since even changing the loading order from before the stores, to the middle, will split the kernel in 2 and potentially break it right now.
I had one specific case when it was an issue when I tried to optimize a software sphere rasterizer, by adding an additional read to check if the atomic min can be skipped I effectively made the compiler think that this part of the code needs to be split into parts and simply just broke the rendering.
This shows that, while powerful, such inference of how the program is structured does not always work, or requires a much more advanced compiler than I have here. On the other hand, in the case of the 2D fluid simulation example, kernel generation worked quite well, since there is no control flow to confuse the compiler.
Optimization and generation of the kernels
Simply splitting the IR into kernel regions is actually not enough to make sure you dont have a million unneeded loads or stores. One very basic way to optimize the kernels is effectively just copying computations that are cheaper to do than to load from memory. Such things like constants, or very simple arithmetic are examples of this. Doing this optimization not only reduces the number of global memory access a lot usually, but also removes a lot of unneeded kernels that would have just stored a constant or something similar into memory.
I also have the standard “removing of unused computation” here. Since we have the entire IR graph from input to ouput given, this additionally allows to figure out which parts of the computation are influencing the outputs. So I can effectively assume that everything else is unused and can be simply removed.
When generating compute kernels out of such an IR, you can not simply use the N dimensional shape of the kernel, and you need to map the tensor indices to the specific layout of the GPU. In this case, that’s the group indices, and the workgroup thread indices (in more advanced cases, in DX12/Vulkan/CUDA/etc there is also the warp sub-group, but I’ll ignore it for now). To do this mapping we ideally would need to figure out the shape of the workgroup, which must be a compile time constant, from the computations we do. But at the moment I simply estimate the group shape from the last 3 dimensions of the kernel, and clamp them to some predefined constants depending on dimensionality. This is suboptimal, but doing it better would either require having a VM that estimates the range of indices of memory accesses, or an autotuner. The first will take some time to implement, and is in my TODO list, as its also useful for other things, and the second, while easier I’m not currenty considering, as it could increase compile times quite significantly. (And they already reach 30 seconds on Windows for my Variational Monte Carlo solver!)
Algorithmic operations
The bare IR does not know about complex operations like matrix multiplication, reductions, etc. These are implemented as a special compiler pass, that converts the high level operation nodes into a series of simpler operations. For example reduction sums tf.sum are converted into a loop of adds, matrix multiplications into a loop of muls and adds, etc.
These simpler operations aren’t yet put into kernels, so the compiler can do additional kernel fusion optimizations on them. As they are written in the same IR and not as separate outside kernels also means that all possible optimizations that that the compiler has - can be applied to them, like inserting simple arithmetic instead of memory loads (useful for operations over procedural data, like random), or adding the activation at the end of the matrix multiplication loop, etc.
(Though to be fair, right now, the compiler optimizes them a bit too aggressively, and can put a lot of needless computation inside a matmul loop for example, this needs to be fixed in the future with better heuristics. Detailed example in IR under the hood section)
Advanced kernel fusion
Kernel fusion by splitting into ranges of the multi-level linked list works fine until you get to more complex situations, that do actually happen quite often in ML, for example, reductions of some expressions.
To optimize even these cases you can do something I call tensor load fusion - you replace a loading operation with the recomputed result of the load target with the given load indices replacing the target kernel indices.
This was tricky to implement, but it allows to fuse operations like tf.sum(A[i,k]*B[k,j], axis=2) into a single 2D kernel, instead of 3D + 2D kernels. This gives a massive speedup in some cases when writing operations in such a naive way. For example this allows you to write out a conv2d operation in a similar form as a sum over a 6D tensor, and the compiler could fuse it into a single 5D reduction + 4D reduction, while giving comparable performance to native pytorch (for small kernels). Here is an implementation in TensorFrost which is effectively equivalent to PyTorch’es conv2d without padding:
def conv2d(X, W):
N, CIN, HI, WI = X.shape
COUT, CIN, h, w = W.shape
bi, cout, wi, hi, cin, it = tf.indices([N, COUT, HI - h + 1, WI - w + 1, CIN, h * w])
i, j = it%w, it/w
return tf.sum(tf.sum(X[bi, cin, wi + i, hi + j] * W[cout, cin, i, j]))
At the moment only the first tf.sum(some operations) gets fused into a single kernel. Which is actually completely fine, as we dont want to merge multiple sum together and we want them to be staged. This is actually why I manually fused the kernel dimensions w and h together, as you need to have a balance between the size of the loop and number of reduction stages. This could theoretically be done automatically, but it would require autotune or more advanced heuristics.
Automatic differentiation
Looking at the example in the section above you might think that autograd would completely fail when differentiating such an expression. Which would be the case if done naively. Whats worse, in the programs I write, loads at addresses are extremely prevalent. If you apply autodiff dirrectly on multidimensional loads you get multidimensional atomic adds. In general, you can’t really do much with them, but in most cases, the indices of the atomic adds are simple, or are constants. In those cases you could check what dimension indices of the operation are not used in the atomic add address computation, and conclude that all threads of this atomic add for this dimension add to the same element. This would mean that we can optimize this by transforming this dimension into a sum over it, with a following atomic add to this element in the end. Even more, you could also check if the indices map 1 to 1, meaning that they do not make conflicting writes, and can just be replaced with a simple load, add and store operation. (However, I don’t actually do this at the moment as nonconflicting atomic adds are cheap enough to be ignored for now)
These optimizations improve performance of automatically differentiated operations of this kind by a lot, and makes prototyping differentiable convolution-like algorithms quite easy. (I’m interested in trying to fine tune a differentiable multi-grid Poisson equation solver, with boundary conditions, by making lots of small convolutions like these)
The rest of the automatic gradient algorithm is your run-of-the-mill backwards mode autodiff. The autodiff pass is before the algorithm insertion pass, so the gradients are computed for high-level operations if possible, as they are usually cheaper and more numerically stable. (And also I don’t have a way to compute gradients of control-flow at the moment, so it works as a substitute for that for now)
Right now gradiets are specified like tf.grad(a,b), and actually, a doesn’t need to be a scalar, the default vector jacobian product (VJP) input is always a 1 no matter the dimensionality of a. This is useful, for instance, when computing gradients of a potential, for instance:
dx = x1 - x2
dist = tf.sqrt(tf.sum(dx**2))
pot = 1.0 / dist
force = - tf.grad(pot, dx)
Quite nice when doing a particle simulation. In fact I also use this when computing the normals for the SDF in my path tracing example.
I should note that this is only valid behaviour because these computations are independent, for pixels, or for particles, if they were depending on each other, the gradient would be invalid, and in that case you should use a scalar a.
The compiler when doing the autodiff searches for all unique a’s and does a full backprop over their dependencies, then all unused gradients are simply removed after this compilation pass.
I still plan to implement forward mode automatic differentiation, in its case its somewhat easier to implement. Since for example I can just do it after all the algorithmic passes, as the form of the computation will be exactly the same as the original, just with slightly different operations.
It does pose the question of what to do when doing a hybrid autodiff, like backward grad of forward grad. In that case the gradients need to be sorted by their order, and done one by one. Unfortunately in this case I would need to implement full jacobian vector product (JVP) (on top of the VJP’s) for all algorithmic operations, not just the base simple non-algorithmic ones, so I’ll probably leave that for the far future.
IR under the hood
Let’s look at how the IR looks in the compiler right now. We will look at the bitonic sort example from above to see how control flow is represented in the IR.
Parsed/traced input
int v1_0 = const(data=[4294967295], )
int element_count = input_shape(flags={InputShapeDim(0), }, )
int keys = memory(flags={Modified, OutputMemory(0), InputMemory(0), }, shape=[element_count], )
int v1_1 = const(data=[4294967295], )
int v1_2 = input_shape(flags={InputShapeDim(0), }, )
int values = memory(flags={Modified, OutputMemory(1), InputMemory(0), }, shape=[v1_2], )
float v1_3 = float(inputs=[element_count], )
float v1_4 = log2(inputs=[v1_3], )
float log2N = ceil(inputs=[v1_4], )
float v1_5 = exp2(inputs=[log2N], )
int Nround = int(inputs=[v1_5], )
int v1_6 = const(data=[2], )
int v1_7 = div(inputs=[Nround,v1_6(2)], )
int sort_id = dim_id(data=[0], shape=[v1_7], )
float v1_8 = const(data=[1065353216], )
float v1_9 = add(inputs=[log2N,v1_8(1.0f)], )
float v1_10 = mul(inputs=[log2N,v1_9], )
float v1_11 = const(data=[1073741824], )
float v1_12 = div(inputs=[v1_10,v1_11(2.0f)], )
int steps = int(inputs=[v1_12], )
int v1_13 = const(data=[1], )
int v1_14 = const(data=[0], )
int step = loop(inputs=[v1_14(0),steps,v1_13(1)], )
{
int v2_0 = const(data=[2], )
int v2_1 = mul(inputs=[v2_0(2),step], )
float v2_2 = float(inputs=[v2_1], )
float v2_3 = const(data=[1065353216], )
float v2_4 = add(inputs=[v2_2,v2_3(1.0f)], )
float v2_5 = sqrt(inputs=[v2_4], )
float v2_6 = const(data=[1056964608], )
float v2_7 = sub(inputs=[v2_5,v2_6(0.5f)], )
float j = floor(inputs=[v2_7], )
float v2_8 = float(inputs=[step], )
float v2_9 = const(data=[1056964608], )
float v2_10 = mul(inputs=[v2_9(0.5f),j], )
float v2_11 = const(data=[1065353216], )
float v2_12 = add(inputs=[j,v2_11(1.0f)], )
float v2_13 = mul(inputs=[v2_10,v2_12], )
float v2_14 = sub(inputs=[v2_8,v2_13], )
float n = round(inputs=[v2_14], )
float v2_15 = sub(inputs=[j,n], )
float v2_16 = exp2(inputs=[v2_15], )
float v2_17 = round(inputs=[v2_16], )
int B = int(inputs=[v2_17], )
float v2_18 = const(data=[1056964608], )
bool v2_19 = lt(inputs=[n,v2_18(0.5f)], )
int v2_20 = const(data=[2], )
int v2_21 = mul(inputs=[v2_20(2),B], )
int v2_22 = const(data=[1], )
int v2_23 = sub(inputs=[v2_21,v2_22(1)], )
int mask = ternary(inputs=[v2_19,v2_23,B], )
int v2_24 = mod(inputs=[sort_id,B], shape=[v1_7], )
int v2_25 = const(data=[2], )
int v2_26 = mul(inputs=[v2_25(2),B], )
int v2_27 = div(inputs=[sort_id,B], shape=[v1_7], )
int v2_28 = mul(inputs=[v2_26,v2_27], shape=[v1_7], )
int e1 = add(inputs=[v2_24,v2_28], shape=[v1_7], )
int e2 = xor(inputs=[e1,mask], shape=[v1_7], )
bool v2_29 = lt(inputs=[e1,element_count], shape=[v1_7], )
bool v2_30 = lt(inputs=[e2,element_count], shape=[v1_7], )
bool v2_31 = and(inputs=[v2_29,v2_30], shape=[v1_7], )
if(inputs=[v2_31], shape=[v1_7], )
{
int key1 = load(memory=[keys], indices=[e1], data=[0], shape=[v1_7], )
int key2 = load(memory=[keys], indices=[e2], data=[0], shape=[v1_7], )
bool v3_0 = lt(inputs=[key1,key2], shape=[v1_7], )
if(inputs=[v3_0], shape=[v1_7], )
{
int val1 = load(memory=[values], indices=[e1], data=[0], shape=[v1_7], )
int val2 = load(memory=[values], indices=[e2], data=[0], shape=[v1_7], )
store(memory=[keys], inputs=[key2], indices=[e1], shape=[v1_7], )
store(memory=[keys], inputs=[key1], indices=[e2], shape=[v1_7], )
store(memory=[values], inputs=[val2], indices=[e1], shape=[v1_7], )
store(memory=[values], inputs=[val1], indices=[e2], shape=[v1_7], )
}
}
}
I made the debug IR representation be somewhat C-like since, at least for me, its easier to read than your usual IR representations. Every line here represents a node in the multilevel linked list. Each {} scope incapsulates all the child nodes of the previous to {} node. While the bitonic sort part is basically just a less readible version of the python code above, we now also have some additional nodes in the IR. Specifically memory, this is the node that represents allocated tensor memory on the device. Here we also see that it has flags signifying that its an output and input of the program. The RemoveUnusedOperations compilaiton stage removes everything that doesn’t influence those memory nodes.
Those of you who know about LLVM would probably question the choices made here, but in my case specifically I was interested in keeping the IR as close to the codegen target as possible, which are C++, CUDA, shading languages, or others. This IR doesn’t really use single assignment form (SSA) or φ nodes, meaning modifications are not versioned. This does pose a problem for autodiff and makes optimization potentially harder, so I do have a compilation pass that can convert at least some in-place operations into versions of the original, in a rather ad-hoc way. I still need to do the same for stores and scatters too, since right now autodiff will usually compute the wrong gradients for these operations, as it doesn’t use the correct version for the gradient, or actually, it simply doesn’t have access to it, because it no longer exists in memory. I have a reason why I dont want to version everything - it will potentially result in overly aggressive additional memory allocation (like imagine this sorting algorithm created a copied version of keys/values every iteration), and you would need to optimize for it separately. But this reasoning could be completely wrong, since I haven’t really worked with LLVM and am not sure about how applicable it might be for my use cases.
After all the compilation stages, the IR creates kernel nodes, replaces multidimensional indexing with flattened 1D indexing, does some optimizations etc.
Final compiled IR
int element_count = input_shape(flags={InputShapeDim(0), InputShapeMemory(0), }, cost=0.000000, )
int keys = memory(flags={Modified, OutputMemory(0), InputMemory(0), }, cost=0.000000, shape=[element_count], )
int v1_0 = input_shape(flags={InputShapeDim(0), InputShapeMemory(1), }, cost=0.000000, )
int values = memory(flags={Modified, OutputMemory(1), InputMemory(1), }, cost=0.000000, shape=[v1_0], )
float v1_1 = float(inputs=[element_count], cost=1.000000, )
float v1_2 = log2(inputs=[v1_1], cost=17.000000, )
float log2N = ceil(inputs=[v1_2], cost=18.000000, )
float v1_3 = exp2(inputs=[log2N], cost=34.000000, )
int Nround = int(inputs=[v1_3], cost=35.000000, )
int v1_4 = const(data=[2], cost=0.000000, )
int v1_5 = div(inputs=[Nround,v1_4(2)], cost=37.000000, )
float v1_6 = float(inputs=[element_count], cost=1.000000, )
float v1_7 = log2(inputs=[v1_6], cost=17.000000, )
float log2N_2 = ceil(inputs=[v1_7], cost=18.000000, )
float v1_8 = const(data=[1065353216], cost=0.000000, )
float v1_9 = add(inputs=[log2N_2,v1_8(1.0f)], cost=19.000000, )
float v1_10 = mul(inputs=[log2N_2,v1_9], cost=38.000000, )
float v1_11 = const(data=[1073741824], cost=0.000000, )
float v1_12 = div(inputs=[v1_10,v1_11(2.0f)], cost=40.000000, )
int steps = int(inputs=[v1_12], cost=41.000000, )
int v1_13 = const(data=[1], cost=0.000000, )
int v1_14 = const(data=[0], cost=0.000000, )
int step = loop(inputs=[v1_14(0),steps,v1_13(1)], cost=141.000000, )
{
kernel(cost=0.000000, shape=[v1_5], )
{
float v3_0 = float(inputs=[element_count], cost=1.000000, )
float v3_1 = log2(inputs=[v3_0], cost=17.000000, )
float log2N_3 = ceil(inputs=[v3_1], cost=18.000000, )
float v3_2 = exp2(inputs=[log2N_3], cost=34.000000, )
int Nround_2 = int(inputs=[v3_2], cost=35.000000, )
int v3_3 = const(data=[2], cost=0.000000, )
int v3_4 = div(inputs=[Nround_2,v3_3(2)], cost=37.000000, )
int v3_5 = block_id(cost=0.000000, shape=[v1_5], )
int v3_6 = const(data=[256], cost=0.000000, )
int v3_7 = block_thread_id(data=[0], cost=0.000000, shape=[v1_5], )
int v3_8 = mul(inputs=[v3_5,v3_6(256)], cost=1.000000, shape=[v1_5], )
int index_0 = add(inputs=[v3_8,v3_7], cost=2.000000, shape=[v1_5], )
bool is_inside_dispatch = lt(inputs=[index_0,v3_4], cost=40.000000, shape=[v1_5], )
if(inputs=[is_inside_dispatch], cost=140.000000, shape=[v1_5], )
{
int v4_0 = const(data=[2], cost=0.000000, )
int v4_1 = mul(inputs=[v4_0(2),step], cost=142.000000, )
float v4_2 = float(inputs=[v4_1], cost=143.000000, )
float v4_3 = const(data=[1065353216], cost=0.000000, )
float v4_4 = add(inputs=[v4_2,v4_3(1.0f)], cost=144.000000, )
float v4_5 = sqrt(inputs=[v4_4], cost=148.000000, )
float v4_6 = const(data=[1056964608], cost=0.000000, )
float v4_7 = sub(inputs=[v4_5,v4_6(0.5f)], cost=149.000000, )
float j = floor(inputs=[v4_7], cost=150.000000, )
float v4_8 = float(inputs=[step], cost=142.000000, )
float v4_9 = const(data=[1056964608], cost=0.000000, )
float v4_10 = mul(inputs=[v4_9(0.5f),j], cost=151.000000, )
float v4_11 = const(data=[1065353216], cost=0.000000, )
float v4_12 = add(inputs=[j,v4_11(1.0f)], cost=151.000000, )
float v4_13 = mul(inputs=[v4_10,v4_12], cost=303.000000, )
float v4_14 = sub(inputs=[v4_8,v4_13], cost=446.000000, )
float n = round(inputs=[v4_14], cost=447.000000, )
float v4_15 = sub(inputs=[j,n], cost=598.000000, )
float v4_16 = exp2(inputs=[v4_15], cost=614.000000, )
float v4_17 = round(inputs=[v4_16], cost=615.000000, )
int B = int(inputs=[v4_17], cost=616.000000, )
float v4_18 = const(data=[1056964608], cost=0.000000, )
bool v4_19 = lt(inputs=[n,v4_18(0.5f)], cost=448.000000, )
int v4_20 = const(data=[2], cost=0.000000, )
int v4_21 = mul(inputs=[v4_20(2),B], cost=617.000000, )
int v4_22 = const(data=[1], cost=0.000000, )
int v4_23 = sub(inputs=[v4_21,v4_22(1)], cost=618.000000, )
int mask = ternary(inputs=[v4_19,v4_23,B], cost=1686.000000, )
int v4_24 = mod(inputs=[index_0,B], cost=622.000000, shape=[v1_5], )
int v4_25 = const(data=[2], cost=0.000000, )
int v4_26 = mul(inputs=[v4_25(2),B], cost=617.000000, )
int v4_27 = div(inputs=[index_0,B], cost=620.000000, shape=[v1_5], )
int v4_28 = mul(inputs=[v4_26,v4_27], cost=1238.000000, shape=[v1_5], )
int e1 = add(inputs=[v4_24,v4_28], cost=1861.000000, shape=[v1_5], )
int e2 = xor(inputs=[e1,mask], cost=3548.000000, shape=[v1_5], )
bool v4_29 = lt(inputs=[e1,element_count], cost=1862.000000, shape=[v1_5], )
bool v4_30 = lt(inputs=[e2,element_count], cost=3549.000000, shape=[v1_5], )
bool v4_31 = and(inputs=[v4_29,v4_30], cost=5412.000000, shape=[v1_5], )
if(inputs=[v4_31], cost=5512.000000, shape=[v1_5], )
{
int v5_0 = const(data=[1], cost=0.000000, )
int v5_1 = sub(inputs=[element_count,v5_0(1)], cost=1.000000, )
int v5_2 = const(data=[0], cost=0.000000, )
int v5_3 = clamp(inputs=[e1,v5_2(0),v5_1], cost=1866.000000, shape=[v1_5], )
int key1 = load(memory=[keys], indices=[v5_3], data=[0], cost=1994.000000, shape=[v1_5], )
int v5_4 = const(data=[1], cost=0.000000, )
int v5_5 = sub(inputs=[element_count,v5_4(1)], cost=1.000000, )
int v5_6 = const(data=[0], cost=0.000000, )
int v5_7 = clamp(inputs=[e2,v5_6(0),v5_5], cost=3553.000000, shape=[v1_5], )
int key2 = load(memory=[keys], indices=[v5_7], data=[0], cost=3681.000000, shape=[v1_5], )
bool v5_8 = lt(inputs=[key1,key2], cost=5676.000000, shape=[v1_5], )
if(inputs=[v5_8], cost=5776.000000, shape=[v1_5], )
{
int v6_0 = const(data=[1], cost=0.000000, )
int v6_1 = sub(inputs=[v1_0,v6_0(1)], cost=1.000000, )
int v6_2 = const(data=[0], cost=0.000000, )
int v6_3 = clamp(inputs=[e1,v6_2(0),v6_1], cost=1866.000000, shape=[v1_5], )
int val1 = load(memory=[values], indices=[v6_3], data=[0], cost=1994.000000, shape=[v1_5], )
int v6_4 = const(data=[1], cost=0.000000, )
int v6_5 = sub(inputs=[v1_0,v6_4(1)], cost=1.000000, )
int v6_6 = const(data=[0], cost=0.000000, )
int v6_7 = clamp(inputs=[e2,v6_6(0),v6_5], cost=3553.000000, shape=[v1_5], )
int val2 = load(memory=[values], indices=[v6_7], data=[0], cost=3681.000000, shape=[v1_5], )
int v6_8 = const(data=[1], cost=0.000000, )
int v6_9 = sub(inputs=[element_count,v6_8(1)], cost=1.000000, )
int v6_10 = const(data=[0], cost=0.000000, )
int v6_11 = clamp(inputs=[e1,v6_10(0),v6_9], cost=1866.000000, shape=[v1_5], )
store(memory=[keys], inputs=[key2], indices=[v6_11], cost=5675.000000, shape=[v1_5], )
int v6_13 = const(data=[1], cost=0.000000, )
int v6_14 = sub(inputs=[element_count,v6_13(1)], cost=1.000000, )
int v6_15 = const(data=[0], cost=0.000000, )
int v6_16 = clamp(inputs=[e2,v6_15(0),v6_14], cost=3553.000000, shape=[v1_5], )
store(memory=[keys], inputs=[key1], indices=[v6_16], cost=5675.000000, shape=[v1_5], )
int v6_18 = const(data=[1], cost=0.000000, )
int v6_19 = sub(inputs=[v1_0,v6_18(1)], cost=1.000000, )
int v6_20 = const(data=[0], cost=0.000000, )
int v6_21 = clamp(inputs=[e1,v6_20(0),v6_19], cost=1866.000000, shape=[v1_5], )
store(memory=[values], inputs=[val2], indices=[v6_21], cost=5675.000000, shape=[v1_5], )
int v6_23 = const(data=[1], cost=0.000000, )
int v6_24 = sub(inputs=[v1_0,v6_23(1)], cost=1.000000, )
int v6_25 = const(data=[0], cost=0.000000, )
int v6_26 = clamp(inputs=[e2,v6_25(0),v6_24], cost=3553.000000, shape=[v1_5], )
store(memory=[values], inputs=[val1], indices=[v6_26], cost=5675.000000, shape=[v1_5], )
}
}
}
}
}
For the most part, the IR here is unchanged, but we have some differences. With the exception of the obviously created kernel under the loop node, we also see that dim_id nodes, which represented the index of an element at this dimension, are replaced with block_id and block_thread_id, on a GPU, for instance, those map to the workgroup index and the internal 3D workgroup thread indices. I didn’t go with a single 1D workgroup thread index, since its somewhat easier to read the generated kernel code, if it maps directly to how compute shaders are written, but this wasn’t really necessary. Additionally the shader compiler might in theory better compile the generated code.
Also notably, by default the compiler clamps all indexing operations to the shape of the memory input to avoid undefined behaviour. Some internal operations can avoid doing this to not do useless work, but I also plan to give the user access to how the indices could be computed under the hood.
There is also the newly appeared cost property of the node, which is only used for evaluating which parts to copy or not in the optimization passes, and mostly serves as a heuristic, and doesn’t represent actual cost of executing a node, that would need to be done in a potential autotuner.
Now, lets look at how higher level operation are compiled right now, for example, a really simple matrix multiplication:
C = (tf.sin(A) @ tf.cos(B.T))**2.0
Which has a pretty simple input IR:
Matmul input IR
int v1_0 = const(data=[4294967295], )
int v1_1 = const(data=[4294967295], )
int K = input_shape(flags={InputShapeDim(1), }, )
int N = input_shape(flags={InputShapeDim(0), }, )
float A = memory(flags={InputMemory(0), }, shape=[K,N], )
int v1_2 = const(data=[4294967295], )
int v1_3 = input_shape(flags={InputShapeDim(0), }, )
float B = memory(flags={InputMemory(0), }, shape=[K,v1_3], )
float v1_4 = sin(inputs=[A], shape=[K,N], )
float v1_5 = transpose(inputs=[B], data=[1,0], shape=[v1_3,K], )
float v1_6 = cos(inputs=[v1_5], shape=[v1_3,K], )
float v1_7 = matmul(inputs=[v1_4,v1_6], shape=[v1_3,N], )
float v1_8 = const(data=[1073741824], )
float v1_9 = pow(inputs=[v1_7,v1_8(2.0f)], flags={OutputMemory(0), }, shape=[v1_3,N], )
Close to the beginning of the compilation all nodes that are marked as Algorithm in the compilers dictionary are replaced with their specific implementations, and after that pass we will be left with an IR like this:
After algorithm insertion
int K = input_shape(flags={InputShapeDim(1), InputShapeMemory(0), }, )
int N = input_shape(flags={InputShapeDim(0), InputShapeMemory(0), }, )
float A = memory(flags={InputMemory(0), }, shape=[K,N], )
int v1_0 = input_shape(flags={InputShapeDim(0), InputShapeMemory(1), }, )
float B = memory(flags={InputMemory(1), }, shape=[K,v1_0], )
float v1_1 = sin(inputs=[A], shape=[K,N], )
int v1_2 = dim_id(data=[0], shape=[v1_0,K], )
int v1_3 = dim_id(data=[1], shape=[v1_0,K], )
float transposed = load(memory=[B], indices=[v1_3,v1_2], data=[0], indexing_mode=Unsafe, shape=[v1_0,K], )
float v1_4 = cos(inputs=[transposed], shape=[v1_0,K], )
int v1_5 = dim_id(data=[0], shape=[v1_0,N], )
int v1_6 = dim_id(data=[1], shape=[v1_0,N], )
float matmul_2 = const(data=[0], flags={Modified, }, shape=[v1_0,N], )
int v1_7 = const(data=[1], )
int v1_8 = const(data=[0], )
int v1_9 = loop(inputs=[v1_8(0),K,v1_7(1)], )
{
float v2_0 = load(memory=[v1_1], indices=[v1_9,v1_6], data=[0], indexing_mode=Unsafe, shape=[v1_0,N], )
float v2_1 = load(memory=[v1_4], indices=[v1_5,v1_9], data=[0], indexing_mode=Unsafe, shape=[v1_0,N], )
float v2_2 = mul(inputs=[v2_0,v2_1], shape=[v1_0,N], )
float v2_3 = add(inputs=[matmul_2(0.0f),v2_2], shape=[v1_0,N], )
set(memory=[matmul_2(0.0f)], inputs=[v2_3], shape=[v1_0,N], )
}
float v3_0 = const(data=[1073741824], )
float v3_1 = pow(inputs=[matmul_2(0.0f),v3_0(2.0f)], flags={OutputMemory(0), }, shape=[v1_0,N], )
As you can see, for the matrix multiplication, it has created a loop that accumulates products like A[i,k]*B[k,j] over k, and transpose is effectively just compiled into a load at transposed indices.
In the future I plan to improve these built-in algorithms to also employ groupshared memory for precaching A and B blocks and sum over them, without this optimization the performance of the matrix multiplication quickly degrades for larger sizes that don’t fit into the cache.
Alternatively, just like in PyTorch, I could simply add natively implemented kernels for these operations, or if I used CUDA, just call cuBLAS, its not even that hard to add. But right now I’m interested in seeing how much I could improve the performance without explicit outside kernels, as it also improves portability, not to mention the fusion. (You don’t have BLAS libraries in graphics API’s unfortunately)
After this compilation pass the kernel generation and fusion happens as well as allocation of memory for the resulting tensor.
Final compiled matmul
int K = input_shape(flags={InputShapeDim(1), InputShapeMemory(0), }, cost=0.000000, )
int N = input_shape(flags={InputShapeDim(0), InputShapeMemory(0), }, cost=0.000000, )
float A = memory(flags={InputMemory(0), }, cost=0.000000, shape=[K,N], )
int v1_0 = input_shape(flags={InputShapeDim(0), InputShapeMemory(1), }, cost=0.000000, )
float B = memory(flags={InputMemory(1), }, cost=0.000000, shape=[K,v1_0], )
float m0 = memory(flags={Modified, OutputMemory(0), }, cost=0.000000, shape=[v1_0,N], )
kernel(cost=0.000000, shape=[v1_0,N], )
{
int v2_0 = block_id(cost=0.000000, shape=[v1_0,N], )
int v2_1 = const(data=[16], cost=0.000000, )
int v2_2 = const(data=[16], cost=0.000000, )
int v2_3 = block_thread_id(data=[0], cost=0.000000, shape=[v1_0,N], )
int v2_4 = block_thread_id(data=[1], cost=0.000000, shape=[v1_0,N], )
int v2_5 = add(inputs=[v1_0,v2_1(16)], cost=1.000000, )
int v2_6 = const(data=[1], cost=0.000000, )
int v2_7 = sub(inputs=[v2_5,v2_6(1)], cost=2.000000, )
int blocks_shape_0 = div(inputs=[v2_7,v2_1(16)], cost=4.000000, )
int v2_8 = div(inputs=[v2_0,blocks_shape_0], cost=6.000000, shape=[v1_0,N], )
int v2_9 = mul(inputs=[v2_8,blocks_shape_0], cost=11.000000, shape=[v1_0,N], )
int v2_10 = sub(inputs=[v2_0,v2_9], cost=12.000000, shape=[v1_0,N], )
int v2_11 = mul(inputs=[v2_10,v2_1(16)], cost=13.000000, shape=[v1_0,N], )
int index_0 = add(inputs=[v2_11,v2_3], cost=14.000000, shape=[v1_0,N], )
int v2_12 = mul(inputs=[v2_8,v2_2(16)], cost=7.000000, shape=[v1_0,N], )
int index_1 = add(inputs=[v2_12,v2_4], cost=8.000000, shape=[v1_0,N], )
bool v2_13 = lt(inputs=[index_0,v1_0], cost=15.000000, shape=[v1_0,N], )
bool v2_14 = lt(inputs=[index_1,N], cost=9.000000, shape=[v1_0,N], )
bool is_inside_dispatch = and(inputs=[v2_13,v2_14], cost=25.000000, shape=[v1_0,N], )
if(inputs=[is_inside_dispatch], cost=125.000000, shape=[v1_0,N], )
{
float matmul_2 = const(data=[0], flags={Modified, }, cost=0.000000, shape=[v1_0,N], )
int v3_0 = const(data=[1], cost=0.000000, )
int v3_1 = const(data=[0], cost=0.000000, )
int v3_2 = loop(inputs=[v3_1(0),K,v3_0(1)], cost=100.000000, )
{
int v4_0 = mul(inputs=[index_1,K], cost=9.000000, shape=[v1_0,N], )
int v4_1 = add(inputs=[v4_0,v3_2], cost=110.000000, shape=[v1_0,N], )
float A_2 = load(memory=[A], indices=[v4_1], data=[0], cost=238.000000, indexing_mode=Unsafe, )
float v4_2 = sin(inputs=[A_2], cost=240.000000, indexing_mode=Unsafe, )
int v4_3 = mul(inputs=[index_0,K], cost=15.000000, shape=[v1_0,N], )
int v4_4 = add(inputs=[v4_3,v3_2], cost=116.000000, shape=[v1_0,N], )
float transposed = load(memory=[B], indices=[v4_4], data=[0], cost=244.000000, indexing_mode=Unsafe, shape=[v1_0,N], )
float v4_5 = cos(inputs=[transposed], cost=246.000000, indexing_mode=Unsafe, shape=[v1_0,N], )
float v4_6 = mul(inputs=[v4_2,v4_5], cost=487.000000, shape=[v1_0,N], )
float v4_7 = add(inputs=[matmul_2(0.0f),v4_6], cost=488.000000, shape=[v1_0,N], )
set(memory=[matmul_2(0.0f)], inputs=[v4_7], cost=489.000000, shape=[v1_0,N], )
}
float v5_0 = const(data=[1073741824], cost=0.000000, )
float v5_1 = pow(inputs=[matmul_2(0.0f),v5_0(2.0f)], cost=6.000000, shape=[v1_0,N], )
int v5_2 = mul(inputs=[index_1,v1_0], cost=9.000000, shape=[v1_0,N], )
int v5_3 = add(inputs=[v5_2,index_0], cost=24.000000, shape=[v1_0,N], )
store(memory=[m0], inputs=[v5_1], indices=[v5_3], cost=158.000000, indexing_mode=Unsafe, shape=[v1_0,N], )
}
}
As you can see, it not only fused the pow at the end of the matrix multiplication, but also fused the transposition with the sin/cos operations into the summation loop. While this impressively created only a single kernel, this isn’t actually super optimal. Matrix multiplcation is often bottlenecked by arithmetic, not just by memory access. And we effectively instead of doing sin/cos N^2 times, do them N^3 times now! This is something that I still need to fine tune in the fusion heuristics algorithm. In the future though, if you could use groupshared caches - it would be fine enough to do the fusion of these input computations at the matrix “block” load stage, this should be enough to significantly reduce the overhead of doing additional sin/cos, as now we do them only for each “block” of the matrix, not for each product. But I would suspect that for huge matrices, these precomputations will still be a bottleneck, and need to be forcibly unfused. So yes, fewer kernels doesn’t actually mean better sometimes.
In the current compiler version I have disabled matmul load fusion completely until I write a better heuristic, as it usually improves performance.
Python frontend
Since I’ve already decided to make a tensor library, I wanted for it to have similar syntax to Numpy and be easily usable from Python. The frontend is a Pybind11 wrapper around the C++ library which overloads all operations in Python.
As this library is effecitively a static compiler, the way you use it is split into 2 parts - the compiled function with “virtual” tensors of potentially undefined shape (but defined dimensionality), and the host, where explicit tensor buffers exist.
Main code
You basically define a function that looks like this:
def matmul():
A = tf.input([-1, -1], tf.float32)
N, M = A.shape
B = tf.input([-1, M], tf.float32)
K = B.shape[1]
C = (tf.sin(A) @ tf.cos(B.T))**2.0
return C
This will be the core of a TensorProgram. You probably noticed that it doesn’t have arguments, right now its a rather ad-hoc way to give the ability to restrict shapes of some inputs to other inputs. Technically I could just parse the function python representation and generate tf.input() automatically, but in either case, you will still need to apply tf.assert_tensor to enforce their shape.
You are probably already asking why its done is such a weird way, but the main goal was the ability to have undefined tensor shapes at compile time, this way you don’t need to recompile the program every time your input changes. This, as you can see, does add some restrictions, since if you don’t do these shape assertions the compiler might not be able to figure out that A and B can actually be multiplied together and will throw an error. I could also have gone with the “assume everything is compatible” route and added assertions in the generated IR automatically before applying the operation, but I suspected such behaviour might have very annoying unintended consequences and could also result in fusion of parts of code that shouldn’t have fused, which would either be wrong, or create assertions that might never be valid and always throw errors. Of course, you can still have the shapes as predefined constants everywhere, in that case this particular quirk becomes rather annoying and more of a hindrence. I suspect that in the future I’ll add support for both automatically reading the function arguments and manual specification like here.
So yeah, the input shape of these tf.input() operations can be -1 for unspecified, and >0 for explicitly specified (or you can use a shape from another input). In some cases having explicit shape might improve performance, as the compiler could do staged reductions and the like.
The way the IR is currently generated is by tracing the Python function, which is significantly easier than parsing Python AST. This does have some interesting side effects. If you do any sort of control flow inside this function, you can only do it with Python values, and on top of that, the result will be unrolled and fixed at compile time.
In fact, all variables, N, M, A, B, etc - are not actual tensors/scalars, but abstractions in the IR, and don’t have a value yet. So doing any kind of print would result in abstract info being spat out, and conversion into Numpy or any other python type would simply be impossible.
As I wanted to have control flow in the IR, I either needed to parse Python AST, or somehow overload existing Python behavour. Initially, all scoped operations, like if or loop took a python function as input, which was quite ugly and very unreadable for deep code, in the same way JAX does it, pretty much. But then I discovered that you can actually overload context manager behaviour. I found this trick in a library for python based shader generation. This means that I can have custom calls at the beginning and end of a section of code, and I could automatically put it as a child scope.
This is what I did, and I overloaded these for some tensor types, so now you can do contol flow in a nicer way! (Arguably still cursed, since now we have 2 ways to make control flow, with different results, not even mentioning that you need to use the .set() method or .val property of a tensor to set its value from these child scopes, as Python doesn’t allow you to overload = operators, and also scatters and stores are fine too)
a = tf.const(0.0)
with tf.if_cond(A == B):
a.val += 1.0
m = tf.const(-1e10)
with tf.loop(begin, end, step) as iteration:
m.val = tf.max(m, data[iteration])
I even used them for custom kernel declaration:
with tf.kernel([M, N, K]) as (i,j,k):
#stuff
You can also use tf.break_loop() to stop the first parent loop. There might be some cases when it doesn’t work, like stopping a CPU loop from within a kernel (what does that even mean?). But usually it works if you don’t do something especially unusual.
Host code
Before anything, you should initialize the backend which will be used, like this:
tf.initialize(tf.cpu) #or tf.opengl
Additionally you can provide the compiler flag for the C++ compiler, like for example:
tf.initialize(tf.cpu, "-g") #or /Di on Windows
After you wrote the main function you can compile it into a TensorProgram like this
matmul_compiled = tf.compile(matmul)
This traces the function into the IR, compiles the IR into kernel form, converts that into C++/Kernel code, compiles that, and links the compiled library at runtime. One of the (not) fun things about this on Windows, is that this requires the Microsoft Visual Studio compiler installed, and on top of that its SLOW as hell, usually at 20x-50x of the IR compilation time. The compiler requires some totally cursed things to set up the env variables to even work, and the command generator ends up looking like this:
ss << "powershell -command \"$VisualStudioPath = & \\\"${Env:ProgramFiles(x86)}\\Microsoft Visual Studio\\Installer\\vswhere.exe\\\" -latest -products * -property installationPath; & cmd.exe /C \\\"\"\\\"\\\"$VisualStudioPath\\VC\\Auxiliary\\Build\\vcvarsall.bat\\\"\\\" x64 && cl "
<< kernelCompileOptions << " /LD " << tempPath
<< sourcePath << " /Fe:" << dllName
<< "\"\"\\\"\"";
I have no clue what is going on here, and thankfully I wasn’t the one who wrote this (you should thank @Devaniti for this one). At least it works.
Linux users win with their gcc in that regard, which is usually also already installed in the system. It is also just 3-4x faster than MVSC.
In the future I want to add Python as an alternative host language (you could also use CUDA too!), as it will speedup the compile times up to 100x, with only slight performance overhead.
These TensorProgram objects take and output TensorMemory buffer objects (you can also give Numpy arrays, or tf.Modules as arguments), which can be created from Numpy arrays like this.
A = tf.tensor(np.zeros([100, 100], dtype=np.float32))
B = tf.tensor(np.zeros([100, 100], dtype=np.float32))
Then you can run the program:
C = matmul_compiled(A, B)
As you can see the inputs are given to the compiled function in the same order as they were executed in the compiled function.
To get the result back into a Numpy array, you can use the Numpy property:
Cnp = C.numpy
Modules
TensorFrost has a simple module system similar to PyTorch, where you can define a module with parameters (that you can optimize by utilizing the modules from tf.optimizers) and a forward function that computes the output of the module as well as a loss function. Neither of these are actually required, but in some cases the optimizers need a specified loss function.
class SmolNet(tf.Module):
def __init__(self):
#specify a custom random scale and offset for the weights when initializing
self.W = tf.Parameter([16, -1], tf.float32, random_scale=0.01, random_offset=0.0)
#dont compute gradients for the bias
self.b = tf.Parameter([-1], tf.float32, optimize=False)
def assert_parameters(self):
#makes sure that the compiler knows that b has shape compatible with W
self.b = tf.assert_tensor(self.b, [self.W.shape[1]], tf.float32)
def forward(self, x):
return x @ self.W + self.b
def loss(self, x, y):
y_pred = self.forward(x, y)
return tf.mean((y - y_pred)**2)
When initializing the module you can add 3 types of TensorFrost accessible parameters:
tf.Parameter- a tensor that will be passed to the TensorProgram as an argumenttf.ParameterArray- a dynamic list of parameters, all of them will be passed to the TensorProgram as argumentstf.Module- another module, all of its parameters will be passed to the TensorProgram as arguments
The shape argument of the parameter can be a list of integers, where -1 means that the shape is not specified yet, and will be inferred from the input tensor. If you need to compute an operation over several tensors of unspecified shape, you need to assert the shapes in the assert_parameters function.
random_scale and random_offset are used to initialize the weights with random values, and are optional, by default the weights are initialized with Xavier initialization for uniform random values.
optimize is used to specify if the parameter should be trained or not, by default all parameters are trainable. This argument does not stop you from computing tf.grad manually, it is just used to specify if the parameter should be updated by the optimizer module.
By itself the module does not do anything, you need to do a second initialization step to either use it inside a TensorProgram, or initialize it as a container for the tensors outside of the program.
def ComputeForward():
model = SmolNet()
#creates tf.input tensors from all the parameters of the module
model.initialize_input()
X = tf.input([-1, -1], tf.float32)
return model.forward(X)
forward = tf.compile(ComputeForward)
model_container = SmolNet()
#creates tf.tensor tensors from all the parameters of the module and initializes them
model_container.initialize_parameters()
#you can change them afterwards too
model_container.W = tf.tensor(np.zeros([16, 100], dtype=np.float32))
X = tf.tensor(np.zeros([100, 100], dtype=np.float32))
#the module is passed as an argument to the compiled function, in the same order as they are created in the function
Y = forward(model_container, X)
model.initialize_input() creates tf.input() tensors for all the parameters of the module. Afterwards assert_parameters is automatically called for this and all child modules. This is useful if you want to use the module inside a TensorProgram, as you can just pass the module as an argument to the compiled function, and all the parameters will be automatically created and the shapes will be asserted.
model.initialize_parameters() creates tf.tensor() tensors for all the parameters of the module and initializes them with random values. This is useful if you want to use the module outside of a TensorProgram, as you can just pass the module as an argument to the compiled function.
This particular part of the library is still quite early stage, mostly only Python-side, and might change a lot in the future.
Optimizer modules
TensorFrost has a set of built-in optimizer modules that can be used to train the parameters of the module.
tf.optimizers.sgd- Stochastic Gradient Descent, has alearning_rateandgrad_clipparameters, default values are 0.001 and 0.0 respectively.tf.optimizers.adam- Adam optimizer, has alearning_rate,beta1,beta2andgrad_clipparameters, default values are 0.001, 0.9, 0.999 and 0.0 respectively.tf.optimizers.rmsprop- RMSProp optimizer, has alearning_rate,decayandgrad_clipparameters, default values are 0.001, 0.9 and 0.0 respectively.
All optimizer modules are initialized with the module as the first argument, and the training hyperparameters as the rest of the arguments.
def OptimizerStep():
X = tf.input([-1, -1], tf.float32)
Y = tf.input([-1, 10], tf.float32)
model = SmolNet()
opt = tf.optimizers.adam(model, learning_rate=0.001, beta1=0.9, beta2=0.999)
opt.initialize_input()
#do a single step of the optimizer (automatically computes gradients and updates the parameters)
L = opt.step(X, Y)
#or
#L = model.loss(X, Y)
#opt.step(L)
params = opt.parameters()
params.append(L)
return params
step = tf.compile(OptimizerStep)
model_container = SmolNet()
opt = tf.optimizers.adam(model_container)
opt.initialize_parameters()
X = tf.tensor(np.zeros([100, 100], dtype=np.float32))
Y = tf.tensor(np.zeros([100, 10], dtype=np.float32))
out = step(X, Y, opt)
opt.update_parameters(res[:-1])
loss = res[-1].numpy[0]
I’ve also recently added regularizers (reg_type = tf.regularizers.l2 or tf.regularizers.l1) and clipping (tf.clipping.norm or just tf.clipping.clip for a clamp), which can be added like:
optimizer = tf.optimizers.adam(model_container, beta1 = 0.0, beta2 = 0.999, reg_type = tf.regularizers.l2, reg = 0.02, clip = 0.01)
optimizer.set_clipping_type(tf.clipping.norm)
Visualization and interactivity
I really wanted a way to output computation results in real time so I decided to add a GLFW + ImGui for a window and simple GUI to the library. (Taichi also did this!) The way it works now is that you can create a window, create the main rendering loop, and then render the tensor as an image. You can do quite a lot of things with this.
#creates a single global window (can only be one at the moment)
tf.window.show(1280, 720, "a window")
while not tf.window.should_close(): #window will close if you press the close button and this will return True
mx, my = tf.window.get_mouse_position()
wx, wy = tf.window.get_window_size()
#simple input example
if tf.window.is_mouse_button_pressed(tf.window.MOUSE_BUTTON_0):
tf.imgui.text("Mouse button 0 is pressed")
if tf.window.is_key_pressed(tf.window.KEY_W):
tf.imgui.text("W is pressed")
#ImGui example
tf.imgui.begin("an imgui window")
tf.imgui.text("some text")
value = tf.imgui.slider("slider", value, 0.0, 10.0)
if(tf.imgui.button("a button")):
print("button pressed")
tf.imgui.end()
#exectute a TensorFrost TensorProgram that outputs a [-1, -1, 3] float32 tensor
img = render_image(...)
#you could also just provide a Numpy array as tf.tensor(), this is usually slower tho, as it requires a GPU upload
#display the image (will be stretched to the window size with nearest neighbor interpolation)
tf.window.render_frame(img)
In this example you have a window rendering loop, inside of the loop you can query the mouse position and the window size. You can also check if a mouse/keyboard button is pressed. You can create simple ImGUI windows, with text, sliders, checkboxes, buttons and plotlines (in the future I want to integrate ImPlot too)
Then to render the frame you pass a tensor to tf.window.render_frame().
Backends
Codegen
I have also written my own code generator here, and right now C++, GLSL and HLSL are supported. Adding additional kernel languages is not very difficult. But right now I still need to refactor the host code generation, as its currently hardcoded to only do C++. The library can actually be run in a purely code generation mode if you don’t need to do any work in Python and would rather integrate it into some other project:
tf.initialize(tf.codegen, kernel_lang = tf.hlsl_lang) # or tf.glsl_lang for OpenGL, or tf.cpp_lang for C++
After you compiled all the tensor programs you need, you can get all the generated code and save it to a file:
# Save all the compiled functions
cpp_header = tf.get_cpp_header()
all_main_functions = tf.get_all_generated_main_functions() #always in C++
with open('tensorfrost_main.cpp', 'w') as f:
f.write(cpp_header)
for func in all_main_functions:
f.write(func)
# Save all the compiled kernels
all_kernels = tf.get_all_generated_kernels() #depends on the kernel_lang
for i, kernel in enumerate(all_kernels):
with open('generated_kernels/kernel_{}.hlsl'.format(i), 'w') as f:
f.write(kernel)
This is also not perfect, ideally I would also provide an example implementation of a runtime, but right now it needs to be written by the user. Also in the future I’d want to compile the TensorPrograms into an archive, that would optionally contain code and compiled binaries, that can be loaded into python immediately. This could be quite useful for debugging code generation in the future.
The generated code right now looks something like this, for the bitonic sort example.
C++ host part
std::tuple<TFTensor> BitonicSort(TFContext tf, TFTensor input0)
{
tf.region_begin("BitonicSort");
int N = input0.shape[0];
tf.check_tensor(input0, "input0", {(uint)N, (uint)2}, TFType::Int);
TFTensor output0 = tf.allocate("output0", {(uint)N, (uint)2}, TFType::Int);
tf.dispatch(0, {output0}, {input0}, {asuint(N)}, {(uint)N, (uint)2}, {2, 16});
float log2N = ceil(log2(((float)(N))));
int Nround = ((int)(exp2(log2N)));
int v4_4 = Nround / 2;
float log2N_2 = ceil(log2(((float)(N))));
int steps = ((int)((log2N_2 * (log2N_2 + 1.0f)) / 2.0f));
for (int step = 0; step < steps; step += 1)
{
tf.dispatch(1, {output0}, {}, {asuint(N), asuint(step)}, {(uint)v4_4}, {256});
}
tf.region_end("BitonicSort");
return {output0};
}
And generated GLSL shaders
//Kernel 1
layout (local_size_x = 2, local_size_y = 16, local_size_z = 1) in;
void main() {
int block_id = int(gl_WorkGroupID.x);
int block_thread_id0 = int(gl_LocalInvocationID.x);
int block_thread_id1 = int(gl_LocalInvocationID.y);
int block_thread_id2 = int(gl_LocalInvocationID.z);
int blocks_shape_0 = ((2 + 2) - 1) / 2;
int vdiv = block_id / blocks_shape_0;
int index_0 = ((block_id - (vdiv * blocks_shape_0)) * 2) + block_thread_id0;
int index_1 = (vdiv * 16) + block_thread_id1;
bool is_inside_dispatch = (index_0 < 2) && (index_1 < var.N);
if (is_inside_dispatch)
{
int input0 = asint(input0_mem[(index_1 * 2) + index_0]);
int output0 = input0;
output0_mem[(index_1 * 2) + index_0] = asuint(output0);
}
}
//Kernel 2
layout (local_size_x = 256, local_size_y = 1, local_size_z = 1) in;
void main() {
int block_id = int(gl_WorkGroupID.x);
int block_thread_id0 = int(gl_LocalInvocationID.x);
int block_thread_id1 = int(gl_LocalInvocationID.y);
int block_thread_id2 = int(gl_LocalInvocationID.z);
float log2N = ceil(log2(float(var.N)));
int Nround = int(exp2(log2N));
int index_0 = (block_id * 256) + block_thread_id0;
bool is_inside_dispatch = index_0 < (Nround / 2);
if (is_inside_dispatch)
{
float j = floor(sqrt(float(2 * var.step) + 1.0f) - 0.5f);
float n = round(float(var.step) - ((0.5f * j) * (j + 1.0f)));
int B = int(round(exp2(j - n)));
int mask = (n < 0.5f) ? ((2 * B) - 1) : B;
int e1 = (index_0 % B) + ((2 * B) * (index_0 / B));
int e2 = e1 ^ mask;
if ((e1 < var.N) && (e2 < var.N))
{
int key1 = asint(output0_mem[(clamp(e1, 0, var.N - 1) * 2) + clamp(0, 0, 2 - 1)]);
int key2 = asint(output0_mem[(clamp(e2, 0, var.N - 1) * 2) + clamp(0, 0, 2 - 1)]);
int val1 = asint(output0_mem[(clamp(e1, 0, var.N - 1) * 2) + clamp(1, 0, 2 - 1)]);
int val2 = asint(output0_mem[(clamp(e2, 0, var.N - 1) * 2) + clamp(1, 0, 2 - 1)]);
if (key1 > key2)
{
output0_mem[(clamp(e1, 0, var.N - 1) * 2) + clamp(0, 0, 2 - 1)] = asuint(key2);
output0_mem[(clamp(e2, 0, var.N - 1) * 2) + clamp(0, 0, 2 - 1)] = asuint(key1);
output0_mem[(clamp(e1, 0, var.N - 1) * 2) + clamp(1, 0, 2 - 1)] = asuint(val2);
output0_mem[(clamp(e2, 0, var.N - 1) * 2) + clamp(1, 0, 2 - 1)] = asuint(val1);
}
}
}
}
I tried to keep the generated code as readable as possible, to some degree it worked, but there are still quite a few ugly parts. I keep all buffers in uint format, as otherwise you can do compareexchange atomics on float elements (at least I think you can’t), so because of this there are a lot of asuint and asfloat/asint all over the place in an average generated kernel.
For this specific example its still quite nice, as we dont have a lot of algorithmic operations or automatically generated autodiff slop.
Runtimes
Right now there are only 2 runtime backends - C++/OpenMP and C++/OpenGL. After the compiler generates the C++ code for the shaders and the host, its compiled by the C++ compiler, and also by the OpenGL shader compiler (which is built in the driver and can have horrible bugs, by the way).
I plan on also adding CUDA and Vulkan in the future, for the first one I could just compile everything, host and kernels into a single .cu file, and its probably relatively straightforward to do (will still need to keep OpenGL for visualization interop), but in the case of Vulkan I would need to write all the boilerplate code for handling basic compute, compiling shaders and memory allocation, that will probably take quite some time.
Examples using TensorFrost
Fluid simulation
Before all the algorithmic Numpy-like stuff, I initially played around with simulations that map nicely to multidimensional arrays, waves and Eulerian (grid based) fluids. For the most interesting example, I implemented a 2D fluid solver with a multigrid pressure solver, RK4 bicubic advection, and vorticity confinement. As this example didn’t require any control flow, but only indexing and basic kernel fusion, it was a nice first test for the compiler.
Also never mind the boundary artifacts or the interpolation issues with the density, its fixable, but I didn’t have enough time to mess around with it. I will probably implement a proper 3D fluid simulation next time anyway.
Fractal path tracer
In this particular case I created my own vec3 class in python here, as without automatic dimension unroll for small constant shape - the compiler will not be able to create a single kernel for it.
Syntactically speaking, this is 1-to-1 the same how I would write a path tracer in a shader, with the exception of there not being any explicit kernel definitions here. I also reused the bicubic interpolation from the fluid example for the camera reprojection, same with the bilinear sampler for the HDRI sky here.
One amazing thing here, is that the normals are computed through backpropagation and not finite differences! It even improved the performance, as FD normals take 4x SDF calculations using the tetrahedron trick, while backwards mode autodiff only takes on the order of 2x. It does only work for unrolled SDF’s like kaleidoscopic iterative fractals (KIF’s), SDF’s that require varying loop iterations or breaks, like Mandelbulb will not be differentiable at the moment.
What about bounding volume hierarchies (BVH) for triangle meshes? Right now you can’t really use them, as the IR does not have a way to declare local arrays, and those will be required for the stack when traversing the BVH tree efficiently (you could actually emulate those with a giant number of local variables and if’s, but why). I suspect I might add those together with groupshared memory, as they will have similar syntax.
At this point, now that I’ve also implemented modules and optimizers, I could also theoretically implement a neural radiance cache here, as I can both train the network and trace the rays. But personally I’d probably prefer a sparse hash grid radiance cache, as its a bit more deterministic.
PS. Looking at the next example, maybe you could use a hash grid + a small neural network together instead, for the radiance cache? This might improve the quality quite a lot
Texture embedder with small neural network
This is very similar to the examples I have done in shadertoy. It’s a small texture, usually 32*32, with an embedding in each pixel. Those embeddings are interpolated at some point in space, concatenated and passed to a small neural network that magically transforms that into a higher resolution image. The interpolation here is also the one from iq’s article “improved texture interpolation”, while that interpolation is “fake” and has 0 gradients at the pixel edges, if you gave the neural net a set of those, but offset by half a pixel, it can actually recreate a proper C2 continuous image without you needing bicubic interpolation! (I didn’t come up with this, all credits to Instant-NGP, Appendix A) Surprisingly, my tests show that bicubic is actually somehow worse at representing images here, than this fake smooth interpolaiton. I suspect the neural net has an easier time at “distorting” bilinearly interpolated values, rather than cubically interpolated ones, as fewer pixels are influenced.
I used my Adam optimizer module to optimize the embedding image and the neural net, given a set of random samples from the original image. Of the interesting things, the gradients of the trilinear interpolation are just atomic adds to a tensor of the same shape as the embedding. It is probably as good as you can do it here anyway, given that the interpolation is at random unordered positions.
N-body SPH with a custom sphere rasterizer
The code for the simulation here is very simple, first computes the SPH densities for each particle using a sum over the gaussian SPH kernels:
i, j, k = tf.indices([N, N, 3])
dx = X[j,k] - X[i,k]
dv = V[j,k] - V[i,k]
def sph_kernel(dist, rad):
return tf.exp(-(dist / rad)**2.0)
# Compute the SPH density
dist = tf.norm(dx)
rho = tf.sum(sph_kernel(dist, sph_rad), axis=1)
And the second part computes the forces, first computes the soft gravity potential, then its negative gradient for the gravitational force. After that it computes the friction (viscosity) and the SPH pressure force, which is the gradient of the SPH kernel times the pressure. There is also the spike force, which is keeping the particles from overlapping to have a nice uniform distribution.
def pressure(rho):
return (rho - rest_density)
# Compute the SPH forces
d2 = tf.unsqueeze(tf.sum(dx**2.0))
dist = tf.sqrt(d2 + 1e-4) # soft distance
Fg = - tf.grad(gravity / dist, dx)
weight = sph_kernel(dist, sph_rad)
weightgrad = tf.grad(weight, dx)
dvdotdx = tf.unsqueeze(tf.dot(dv, dx)) / (tf.sqrt(d2) + 1e-5)
Fvisc = - viscosity * dvdotdx * weightgrad
Fsph = stiffness * 0.5 * (pressure(rho[i]) + pressure(rho[j])) * weightgrad
dist2 = (tf.sqrt(d2) + 1e-8)
Fspike = - 250.0 * sph_kernel(dist, 1.0*sph_rad) * dx / (dist2*dist2)
Fij = tf.select(i == j, 0.0, Fg + Fsph + Fvisc + Fspike)
Fi = tf.sum(Fij, axis=1)
Vnew = V + Fi * dt
Xnew = X + V * dt
And thats about it! The compiler actually fuses all these operations and the sum into a single loop, meaning there are only 2 kernels here, 1 for the SPH densities, and another for the forces.
The second part of this example is the rendering, which was also written purely in TensorFrost. Its a custom atomicMin (tf.scatterMin) rasterizer, which does a loop over all the pixels each particle sphere occupies on the screen, which is done by projecting the particle position onto the screen and doing atomic mins with a packed value high bits of which contain the depth, and low bits contain its index. The last pass after this one is the final shading, it computes the normals of each sphere, and computes its color.
Neural Cellular Automata
I always wanted to recreate the results of the Growing Neural Cellular Automata article, as the way the model worked was very similar to some shadertoys I did!
While implementing it there were some problems with unrolled iterations, the number of kernels got so huge some of the fused ones accessed more buffers than OpenGL supports, which led to a compilation fail. I manually restricted fusion for this to not happen by doing a “hack”. I did that by introducing a .stop_fusion() method, which is absolutely hilarious given fusion was our initial goal. I guess it would be better to have an automatic way to restrict kernel size in the future.
Ideally I’d want the compiler to be capable to take gradients of loops natively so that it doesn’t generate a thousand kernels, but thats for the future I guess. Right now I keep the iteration count at around 30, while the original used 60-90 as far as I remember. Increasing the fire rate does reduce the required iteration count, as it “technically” increases the average time-step of the simulation, so I did just that.
In my own implementation I did a few changes compared to the original paper, notably I’ve added a laplacian input kernel, as it actually reduces checkerboard artifacts and improves convergense quite drastically. Sobel kernels have a step size of 2*dx, while the laplacian kernel has dx which makes it more accurate. It can also now natively emulate diffusion equations, before it needed to do gradients of gradients to do that.
Also I’ve added quantization and clamping of the fields, which allowed it to be ported to Shadertoy. Surprisingly it also seems to improve training convergence, perhaps due to more normalized channels.
More examples are in the examples folder.
What’s the current performance compared to other tensor libraries?
I’ll focus on comparing things that are easy to implement in both my library and in PyTorch/JAX. Things like the fluid sim or path tracer, I suspect, have no chance of running good if at all in PyTorch, JAX however might work fine with vmap, but I’m not sure. For these tests, I’ll ignore these use cases, as they will not be easy to port to them anyway, given the quite different syntax (as I didn’t write those vectorized, but more in “shader-like” code)
N-body simulation
One of the simplest simulations you can do - is a N-body gravity simulation, which only takes a dozen lines both in TensorFrost, JAX or PyTorch, making this a nice benchmark.
dx = tf.unsqueeze(X, axis=1) - tf.unsqueeze(X, axis=0)
d2 = tf.unsqueeze(tf.sum(dx**2.0, axis=-1), axis=-1) + 1e-4
dist = tf.sqrt(d2)
Fg = -dx * 1.0 / (d2 * dist)
Fi = tf.sum(Fg, axis=1)
Vnew = V + Fi * 0.001
Xnew = X + Vnew * 0.001
This is basically all there is to it, but if you don’t do kernel fusion, you will perform hillariously bad here, as lots of N^2 buffers will be allocated and waste a lot of bandwidth, but just for a demonstration, here is how default eager mode evaluation PyTorch scales compared to TensorFrost:
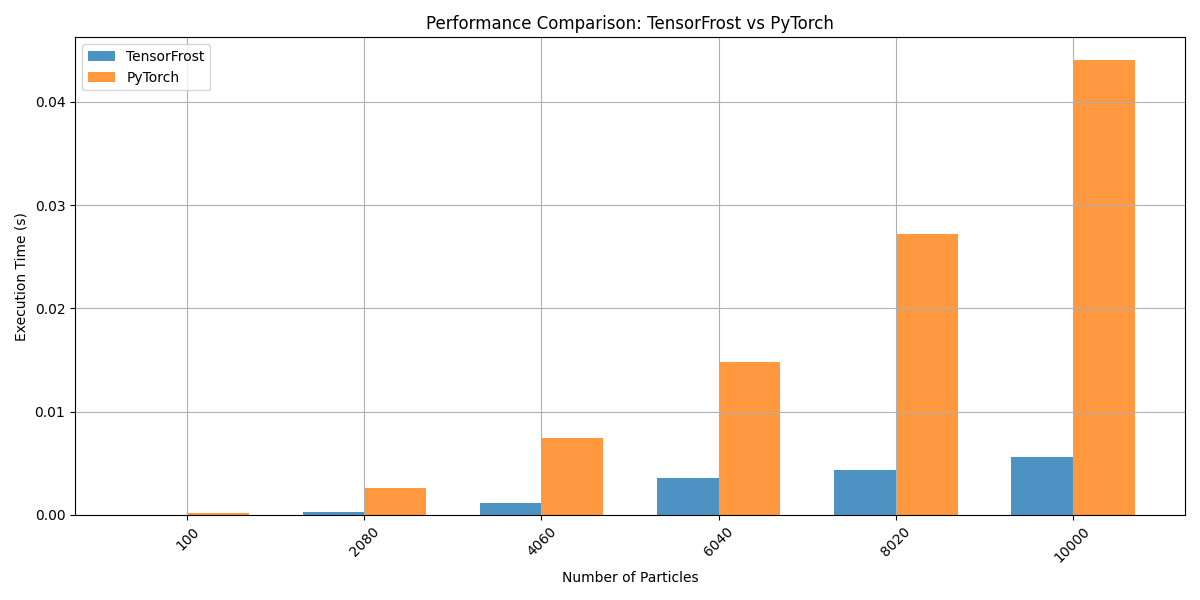
It is very bad, but this is quite expected, we aren’t fusing any kernels here. Let’s now compare it to compiled PyTorch, and to compiled JAX. (All tests done on Ubuntu/RTX 2060/CUDA)
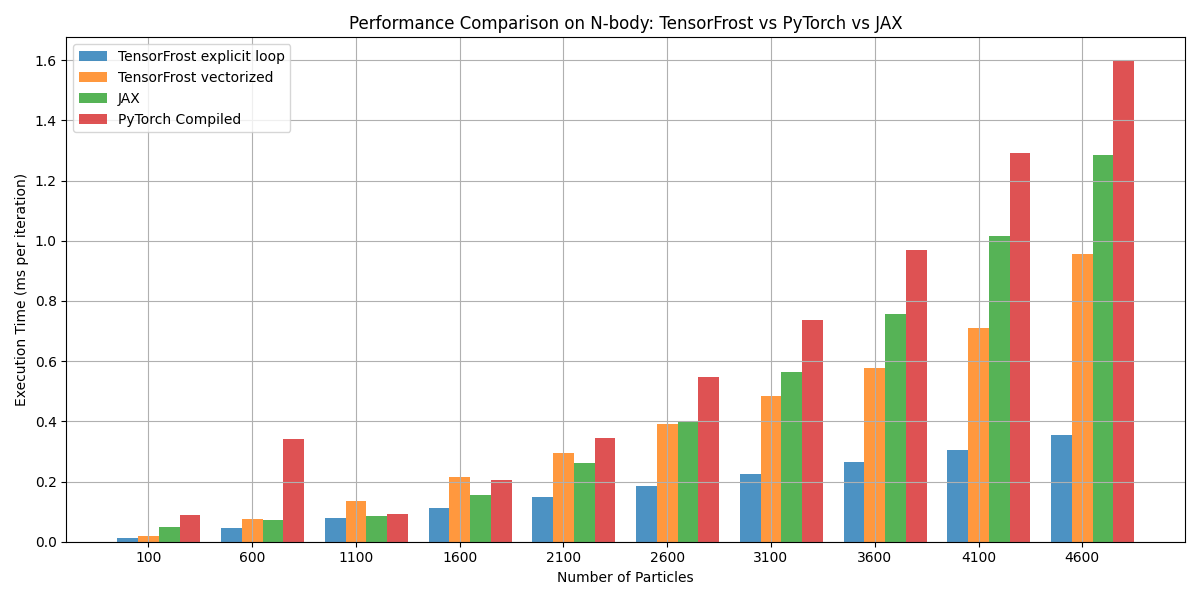
The results here are quite surprising, first of all, the compiled version of the function both in Torch and JAX are very close to what TensorFrost achieves here, which I actually didn’t expect, in some cases they even win, like ~1000 particles. But they still scale slightly worse than the TensorFrost version of the same code curiously. Do they employ some staged reduction here?
TensorFrost doesn’t actually fuse these operations 100% optimally here, the final generated kernel does 1 thread per each resulting component of the force. Ideally you’d do a single loop for all components, as they easily fit in the registers, and you remove a lot of wasted computations. This is the explicit loop version of the same calculations. The code looks like this:
Fi = tf.buffer([N, 3], tf.float32)
i, = tf.indices([N])
Fix, Fiy, Fiz = tf.const(0.0), tf.const(0.0), tf.const(0.0)
x0, y0, z0 = X[i, 0], X[i, 1], X[i, 2]
with tf.loop(N) as j:
x, y, z = X[j, 0], X[j, 1], X[j, 2]
dx, dy, dz = x - x0, y - y0, z - z0
d2 = dx*dx + dy*dy + dz*dz
dist = tf.sqrt(d2 + 1e-4)
Fg = -dx / (d2 + 1e-4) * 1.0 / dist
Fix.val += Fg * dx
Fiy.val += Fg * dy
Fiz.val += Fg * dz
Fi[i, 0] = Fix
Fi[i, 1] = Fiy
Fi[i, 2] = Fiz
Vnew = V + Fi * 0.001
Xnew = X + Vnew * 0.001
And unsurprisingly it absolutely demolishes every other contestant by a factor 2-3x at the cost of uglier code.
However, this is still nowhere near what a hand-tuned shader version of this would do. As you can actually do block reductions here. Preload a range of particles into groupshared, then do the force computation for this block, and repeat for the next blocks. You can do even better, if you preload something like 4-8 particles into registers, and compute their forces from there, leading to a staged block algorithm. This is how you usually try to optimize reductions that reuse a lot of memory, like matrix multiplications.
Of course, something like Taichi would actually win here against everyone, but its not our comparison target as you can’t write the simulation in vectorized tensor form there, and likely after I implement automatic groupshared cache generation the performance gap might go to 0, or become better, tho I suspect probably not without some really advanced heuristics.
MNIST with a convolutional network
–Link to equivalent PyTorch example–
After I implemented module support with the optimizers, first thing I made is a convolutional neural net for the Fashion MNIST classification problem. This is a more classic ML problem and you would probably expect for PyTorch to just straight up win every time. Turns out, actually no, for small network sizes, TensorFrost can actually have a significant win.
Here is a comparison of the number of training iterations per second for the same minibatch size of 128 and with the same(ish) ADAM optimizer, for TensorFrost and for PyTorch
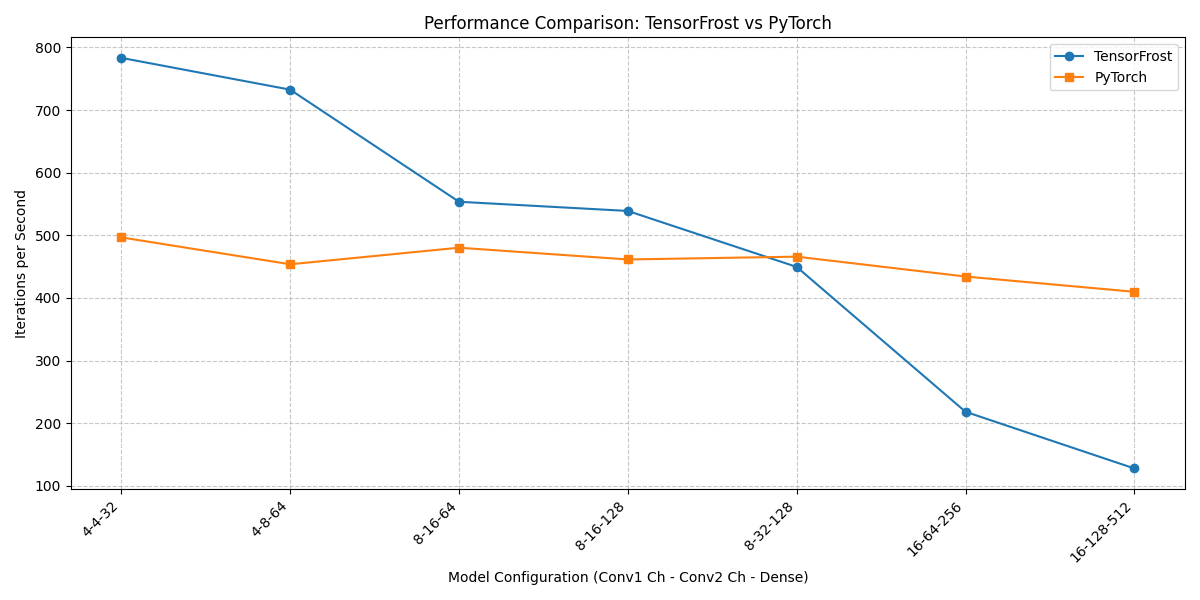
For really tiny networks there is a large win, and the performance drops linearly with more channels/neurons, and at around 8-32-128 becomes slower than eager mode PyTorch. I also have tried compiled PyTorch, but it somehow became slower, did they mistakingly fuse some things incorrectly? I don’t know. I also haven’t tried JAX here, but I suspect its probably somewhat faster than PyTorch. I also wonder if you can compile a training step in PyTorch, thats something that TensorFrost does by defaut, and it’s not a very fair comparison without it.
Honestly speaking, I’m not sure If the win that TensorFrost has at small sizes is due to just having less overhead, or due to better kernels at small size. It might also be that the training step in PyTorch has huge overhead for the minibatch creation. In TensorFrost I have the entire dataset on GPU and use it directly without intermediate steps.
As a bonus I captured the TensorFrost 16-128-512 pass in Nvidia Nsight, with debug regions (ran on RTX 3090)

PS. It’s pretty annoying to benchmark these, as I usually work on Windows (arguably better for graphics dev), rather than on Linux, and the compiled GPU versions of JAX/PyTorch are only available on Linux. TensorFrost works on both platforms, and it is actually easier to port from Windows to Linux than the other way around
What about some more advanced models?
While I could have also tested something like LLM’s or diffusion models, I can pretty much guarantee that for anything that has its bottleneck in matrix multiplication or other linear algebra algorithms TensorFrost will very likely lose by a lot, at least without implementing automation of more advanced optimizations or without just calling external BLAS libraries like cuBLAS, which is doable, but I unfortuanately don’t have enough time to do that, as I focus more on just the compiler itself because its more important for my use cases.
What is left to do
1. Better handling for small constant shapes
One of the things that quite often happens with writing vectorized code for simple particle simulations, like the simple N-body example from above, is that all the vector variables are 3d, and can easily be stored in registers, but the current compiler will generate it as a […, a, b, 3] shaped kernel with a lot of duplicated arithmetic (unless you create your own vec class that operates only on scalars). This is something that could be optimized in the future, by generating the initial kernel with a smaller shape, like […, a, b, 1] and then unrolling the dimensions that are broadcast compared to the kernel’s shape.
Even more advanced optimizations can be performed from that starting point, like automatic caching of data into groupshared memory. Such a caching would require automatic read/write range analysis, for that I will need to implement a VM that executes the operations and computes the range of values they can have with interval arithmetic (perhaps more complex analysis too).
2. Improved workgroup utilization
At the moment the IR does not have a representation for groupshared memory, which is a big bottleneck for large matrix multiplications, and can be quite useful for optimizing some other algorithms, like FFT/sort/convolutions.
Kernels can be additionally fused at the workgroup level as a post kernel fusion pass, which is quite complicated, and requires additional groupshared memory with group syncs, and a correct estimation of the group size, but for small neural networks it could be a massive speedup.
3. Automatic vectorization
One nice thing, that I would like to borrow from JAX is vmap. Writing particle simulations in vectorized form often annoyingly require a lot of squeeze and unsqueeze operations, which could be automated if you vectorized a single particle calculation into a target shape. In fact, I could also make the explicit kernel node usage assume that all its children are scalar (if not - unroll), and it would also behave similarly to vmap with the exception of it forcibly creating a single kernel no matter what. Implementing vmap is, I supect, not to difficult, as it only requires padding all the shapes of the child operation with the given shape (with some peculiarities). Syntactically it could look like
with tf.vmap(shape) as (i,j,...):
#stuff
With i,j,k being scalar at trace time, then padded with given shape.
4. Better IR?
Another thing that is perhaps very high in the priority list right now is to implement repeating computation eliminator, its quite troublesome due to requiring some way to compare entire computation chains (by making a specific computation result node have a unique number), but would remove quite a lot of redundant cruft from the generated kernels.
And on top of that the compilation time scales quadratically with Tensor Program size right now. This is something that I have started to notice with the more complex projects that I tried to do here, like Variational Monte Carlo or Neural Cellular Automata. The number of generated kernels there reaches hundreds, and for NCA sometimes even thousands due to unrolled iteration loop.
While this wasn’t really an issue for most of the simpler stuff, where it was usually bottlenecked by the shader/c++ compiler, this will become a problem for more serious projects in the future.
The way the compiler is written is still very sub-optimal, and more at a research-grade state at the moment. Some operations over every kernel require a complete update of the IR which clearly will make it scale quadratically. This is clearly due to me not having the required experience to properly write a good data structure for a compiler.
So perhaps replacing my own IR with LLVM could make more sense in the long run, though I’m still not sure about the specifics, and how easy it would be to integrate.
5. Documentation
Right now the only documentation is provided in the README.md file in the repository, in the future I should made a separate documentation page for this.
6. Easier debugging / profiling
While ideally I would have wanted the compiler to generate optimal or close to optimal programs - this is still very much not the case, and some simple things like using/not using reshape might change the performance by an order of magnitude just due to, for example, some reductions now being over one dimension instead of several and the compiler not having a way to optimize this scenario (this was a problem in NCA).
Ideally I’d expose the compiled result in a more readible / easy to access way. Perhaps something like giving the ability to compile the program purely into its IR, so that you can edit it, for example.
7. More test cases
Compiler tends to fall apart when trying to implement a completely new thing right now - this was kind of expected to be honest, without a large enough set of tests it is almost guaranteed that it will fall apart at some edge cases, and the only way to fix this is just to make a whole lot of example projects which I’m currently working on bit by bit
8. Improve the GLFW/ImGui integration
I only passed the bare minimum for these to be able to make basic windows and GUI, but ideally all their features should be exposed. This is quite a large task and will take a lot of time I suspect. I also want to integrate ImPlot for much better plots, as for real-time use cases I think those will be more useful than matplotlib.
9. Generate python code for the host part of the program
As usually the compilation bottleneck is the C++ compiler, I’m considering to just use Python for the kernel dispatch code. This might reduce the performance a bit, but for faster iteration this is certainly going to be useful.
10. A whole bunch of basic Numpy functionality is still missing
Things like concatenation/stacking/splitting/repeat/etc does not exist yet, and I currently emulate them manually by reindexing, which works but is tedious.
Something like a random number generation module would be quite useful. As they are stateful I want to expose all their internals to the user so I think making them in the form of a tf.Module makes sense. So something like rng = tf.random.rng_module(type=..., seed=...) I suppose. Which you use then like rng.unform(2.0,3.0,shape) or other. You could then pass them around as parts of bigger modules together with their seeds.
Linear algebra algorithms, like QR, SVD, LU, eigendecomposition, inverse, determinants, etc, are not part of the library, which is an issue for more complex data analysis and algorithms. Unfortunately these are very hard to implement from scratch, espectially with any resemblence of performance or numerical precision. So I suppose I have no choice but to use an external library for these in the future.
And there are other ones like FFT, sorting etc. Tho I have them implemented in the examples, I just need to integrate them into the library.
11. More tensor formats
Right now we only have int32, uint32, float32 and bool, which is not many. Something like custom quantized formats that Taichi provides would be very nice to have. Adding the option to pack the last dimension if its constant and small with custom packing would also allow quantized vectors of sorts, the shared exponent format is very useful for simulations.
Perhaps also specifying the behaviour of the tensor on out-of-bounds reads/writes could be nice to add to the format, as the default one is just clamp.
Adding support for HW supported GPU texture formats would be nice for rendering algoirhms, as tensors which are represented as textures will have performance benefits for render-like use cases, not to mention the optional ability to use the HW linear sampler.
There are probably a million more things that I forgot, but even without those, this is enough work for years to come.
Conclusion
Making a compiler with practically 0 compiler development experience was certainly quite the gamble. I’m 100% sure there are some fundamental architectural decisions that I did wrong, the main of it being perhaps writing the IR from scratch, as I had no clue how LLVM worked even tho I knew that it is used everywhere, and probably for a very good reason. Writing the compiler like that took an astounding amount of time, while initially I’ve expected a few months of work, now I’m at 14 months and some core features I wanted are still missing.
Quite often it was hard to convince myself that this is a useful use of my time, the scope of work is so huge that making progress felt like an eternity, and I could have instead spend that time on making other pet projects. Even now, I can not easily explain why exactly I wanted to make a library/compiler like this, as there are hundreds of little things that come together to make it useful for what I do, and I hope this blog post explains at least some part of my thought process here.
Right now the library is at the point of being somewhat usable. In fact, given the performance tests from above, if you properly improved the performance of the algorithmic primitives I use, like reductions and matmuls, and added more backends like CUDA, this library or a new version of it might become a viable choice for more common ML applications.
If anyone wants to help me with development, PR’s are welcome! There are still like a million things missing, lots of hidden bugs waiting to be found, and by myself it would take a few more years for it to get into a more mature state.
Why TensorFrost?
The name was chosen from "tensor" + my surname translated from Ukrainian to English. I know, its not super creative, given how many "TensorSomething" already exist. Also there is the funny problem that LLM's mistakingly assume its TensorFlow. Perhaps I should do `import TensorFrost as fr` instead of `as tf` in my examples.
